|
Question 1208458: Determine this function is increasing, decreasing, even, odd, and/or invertible on its natural domain
 .
I think I've already found that this is odd, because f(-x) = (-x)/((-x)^2+1) is clearly also equal to -f(x) = -x/(x^2 + 1), but I have having trouble finding whether this is increasing or decreasing.
I know:
increasing is when the gradient of the tangent is positive
and decreasing is when the gradient of the tangent is negative, but I need help finding this.
I am also already pretty sure there is no inverse.
Found 3 solutions by Edwin McCravy, ikleyn, math_tutor2020:
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!
Yes. it is an odd function.
A look at the graph tells us that it decreases asymptotically to a minimum
on the left, then increases to a maximum, then decreases asymptotically again.
But we must show that.
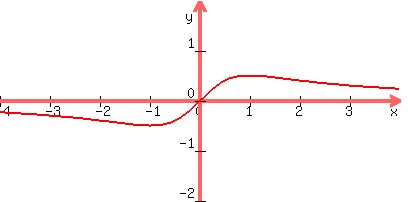We find the extreme values:
 .
 .
 .
 .
We see that = 0 to find the extremum points.
The solutions are x=1, x=-1
Checking a test point, say, x=-2, on interval (-inf,-1) we find
that the gradient of the tangent (the derivative) is negative, so
it is decreasing.
Checking a test point, say, x=0, on interval (-1,1) we find
that the gradient of the tangent (the derivative) is negative, so
it is increasing. Thus there is an absolute minimum point at x=-1
Thus we know that f(x) is decreasing on (-infinity,-1).
Checking a test point, say, x=2, on interval (1,infinity) we find
that the gradient of the tangent (the derivative) is negative, so
it is decreasing. Thus, there is an absolute maximum point at x=1
So f(x) is
1. decreasing on the interval (-infinity,-1)
2. increasing on the interval (-1,1)
3. decreasing on the interval (1,infinity)
We can show that it is not invertible by showing that f(0.5) = 0.4 = f(2).
Thus f(x) is not one-to-one.
Edwin
Answer by ikleyn(52767)  (Show Source):
You can put this solution on YOUR website! .
Edwin produced a perfect/irreproachable solution for you.
To it, I want to add very attractive logical reasoning to determine the behavior of the function.
Let's look into the function in the first quadrant x > 0.
The function is positive there, since both the numerator and the denominator are positive at x > 0.
Next, you see that the function tends to zero as x goes to +infinity.
Also, you see that the function tends to 0 as x goes to 0.
So, the function is zero at zero and at infinity and is positive everywhere else.
From the theorems of Calculus, it means that the function has a local maximum
(may be, several maximums) somewhere between x= 0 and infinity.
It is exactly what you see in the plot.
Unfortunately, this reasoning can not determine, how many maximums are there
and what are their positions.
For it, the analysis similar to that Edwin provided for you is necessary.
After that as you analyzed the function behavior in the 1st quadrant,
you can extend your conclusions about its behavior in the 3rd quadrant, using the odd symmetry.
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
I'll show another way to prove that x/(x^2+1) is odd.
Claim: If p(x) is odd and q(x) is even, then r(x) = p(x)/q(x) is odd.
Proof:
p(-x) = -p(x) ...... since p is odd
q(-x) = q(x) ...... since q is even
r(x) = p(x)/q(x)
r(-x) = p(-x)/q(-x) ...... after replacing each x with -x
r(-x) = -p(x)/q(x) ...... apply rules shown above
r(-x) = -r(x)
Therefore, r(x) is odd.
Using that idea we can show f(x) = x/(x^2+1) is odd since x up top is odd, while x^2+1 down below is even.
An odd polynomial has all of its exponents as odd integers.
An even polynomial has all of its exponents as even integers. Think of the +1 at the end as x^0.
|
|
|
| |
