SOLUTION: The safe load, L, of a wooden beam supported at both ends varies jointly as the width, w, and the square of the depth, d, and inversely as the length, l. A wooden beam 8in. wide,

Algebra ->  Real-numbers -> SOLUTION: The safe load, L, of a wooden beam supported at both ends varies jointly as the width, w, and the square of the depth, d, and inversely as the length, l. A wooden beam 8in. wide,      Log On


   

Question 1208451: The safe load, L, of a wooden beam supported at both ends varies jointly as the width, w, and the square of the depth, d, and inversely as the length, l. A wooden beam 8in.
wide, 8in.
deep, and 5ft
long holds up 15106lb
. What load would a beam 9in.
wide, 5in.
deep, and 18ft
. long, of the same material, support? Round your answer to the nearest integer if necessary..

Found 2 solutions by josgarithmetic, greenestamps:
Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
Exactly as the written language works,
but first you have a problem in the written description. You should not use a variable "l". You already have a upper case L for "load". The lower case "L" looks like digit 'one'. Letting p be this "length", then the description so changed becomes:
L=kwd%5E2%281%2Fp%29


Some of the given data allows you to find the value of k.

Lp=kwd%5E2
%28Lp%29%2F%28wd%5E2%29=k

Using the given data, k=%2815106%2A5%29%2F%288%2A8%5E2%29
k=147.5, which is approximate.

Your formula is L=147.5%28wd%5E2%29%2Fp

---

If w=9 inch, d=5 inch, p=18 feet, then L would be
%28147.5%2F18%29%289%2A5%5E2%29
.
.

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


If you are going to find the safe loads for several different sets of parameter values, then do as the other tutor says and use the given information to determine the proportionality constant k, and then use the formula and that value of k to find the safe loads for the other sets of parameter values.

If you only need to find the answer to this single problem, there is no need to determine the proportionality constant.

For the given set of parameter values, the safe load is 15106 pounds.

The safe load varies directly as the width of the beam. From the given set of parameters to the new set, the width changes by a factor of 9/8, so that change in the width changes the safe load by a factor of 9/8.

The safe load varies directly as the square of the depth of the beam. From the given set of data to the new set, the depth changes by a factor of 5/8, so that change in depth changes the safe load by a factor of (5/8)^2 = 25/64.

The safe load varies inversely as the length of the beam. From the given set of data to the new set, the length changes by a factor of 18/5, so that change in length changes the safe load by a factor of 5/18.

So the combination of changes in the parameters changes the safe load by a factor of

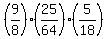
%289%2F8%29%2825%2F64%29%285%2F18%29

So the safe load with the new set of parameters is

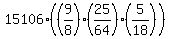
15106%28%289%2F8%29%2825%2F64%29%285%2F18%29%29

Use a calculator to find the safe load with the new set of parameters is, to the nearest pound, 1844 pounds.