SOLUTION: On a library shelf there are 7 different science books and 5 different math books. Find the number of ways to arrange the books next to each other on the shelf if no two math boo

With 7 Science book on the bookshelf, we have 6 + 1 + 1 = 8 possible positions for the Math books
(6 positions between the Science books, one position on the left and one position on the right).


So, the number of all different placements of 5 different Math books is  

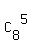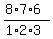     =  = 8*7 = 56.


We should multiply it by  7! = 1*2*3*4*5*6*7 = 5040 (the number of permutations of 7 Science books)
and by 5! = 120 (the number of permutations of 4 Math books).


So, the final answer is  56*5040*120 = 33,868,800.