|
Question 1208377: Find the equation of the circle passing through the points (1,2),(3,6),(5,4).
Found 5 solutions by josgarithmetic, ikleyn, timofer, math_tutor2020, MathTherapy:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
90% of "solutions" produced by @josgarithmetic at this forum are INCORRECT.
This one is not an exclusion: it is INCORRECT, too.
His equation  + + 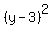 = 5 is wrong. = 5 is wrong.
To convince yourself, check the point (3,6).
My advise to all visitors is: do not even touch his solutions.
Blindfold your eyes and plug your ears so as not to see
and not to hear his absurdist solutions.
They all are toxic and dangerous for your mental health.
This person does not know elementary Math, despite his
self-praise description in his self-description section.
The amazing fact is that he gets a huge amount of applauses and gratitude
from his fans for his wrong solutions, which I cannot understand at all.
Loud, unceasing applause, everyone stands up, ovation.
It tells a lot about mathematical level of his admirers (which level is about zero from the negative side).
People call this level "below the baseboard".
---------------------
Thanks to god, after seeing my reaction, he removed his absurdist solution
from his post, which is good. So, my protest was effective, is counted,
and I successively cleaned the Internet.
@josgarithmetic, your solution method was wrong
independently on drawing the points on graph.
There is no need to draw the points on graph to see
that your solution method is wrong.
It is/was wrong by itself.
Answer by timofer(105)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 
Explanation
Let
A = (1,2)
B = (3,6)
C = (5,4)
The order of the points does not matter.
The labels are there to help set up the other items mentioned in this solution page.
The circle you're trying to find is known as a circumcircle aka circumscribed circle.
The circumcenter is the center of the circumcircle.
The circumcenter is at the intersection of the perpendicular bisectors.
Check out this page to see how to find the equation of the perpendicular bisector of AB.
That page concludes with the equations x+2y=10 and y=(-1/2)x+5.
The equation I'll use is x+2y=10.
Follow a similar process to determine an equation for the perpendicular bisector of BC is x-y=-1.
Solving this system  will pinpoint the circumcenter. will pinpoint the circumcenter.
Subtract the equations.
This is to cancel the x terms so you can solve for y.
You should get 3y = 11 which solves to y = 11/3.
This is the y coordinate of the center of the circle.
Plug y = 11/3 into either x+2y=10 or x-y=-1. Solve for x. You should get x = 8/3.
I'll leave the scratch work for the student to do.
The center of the circle is located at (h,k) = (8/3,11/3)
h = 8/3 = 2.6667 approximately
k = 11/3 = 3.6667 approximately
For each decimal the '6's go on forever but we have to round at some point.
So we have the center of this circle.
We now need the radius.
Use the distance formula

to calculate the distance from the center (8/3,11/3) to any of the three points A,B or C.
This will yield the radius r.
I'll let the student do the scratch work.
You should get 
Square both sides to get 
Side note:  approximately and approximately and  approximately approximately
The decimal 5.55556 should have the '5's go on forever, but we have to round at some point.
--------------------------------------------------------------------------
Summary:
(h,k) = (8/3, 11/3) is the center
 is the radius which has both sides square to is the radius which has both sides square to 
The circle template  updates to the final answer updates to the final answer 
You can verify by using GeoGebra or Desmos
There are many other similar tools.
Another way to verify would be to plug the coordinates of points A,B,C into the answer equation. Simplifying everything should lead to the same number on each side.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the equation of the circle passing through the points (1,2),(3,6),(5,4).
We start with:  <==== Standard form of the equation of a CIRCLE:
Point: (1, 2) <==== Standard form of the equation of a CIRCLE:
Point: (1, 2)
 ---- Standard form of the equation of a CIRCLE ---- Standard form of the equation of a CIRCLE
 ---- Substituting (1, 2) for (x, y)
1 - 2h + h2 + 4 - 4k + k2 = r2
h2 - 2h + k2 - 4k + 5 = r2 ----- eq (i)
Point: (3, 6) ---- Substituting (1, 2) for (x, y)
1 - 2h + h2 + 4 - 4k + k2 = r2
h2 - 2h + k2 - 4k + 5 = r2 ----- eq (i)
Point: (3, 6)
 ---- Standard form of the equation of a CIRCLE ---- Standard form of the equation of a CIRCLE
 ---- Substituting (3, 6) for (x, y)
9 - 6h + h2 + 36 - 12k + k2 = r2
h2 - 6h + k2 - 12k + 45 = r2 ----- eq (ii)
Point: (5, 4) ---- Substituting (3, 6) for (x, y)
9 - 6h + h2 + 36 - 12k + k2 = r2
h2 - 6h + k2 - 12k + 45 = r2 ----- eq (ii)
Point: (5, 4)
 ---- Standard form of the equation of a CIRCLE ---- Standard form of the equation of a CIRCLE
 ---- Substituting (5, 4) for (x, y)
25 - 10h + h2 + 16 - 8k + k2 = r2
h2 - 10h + k2 - 8k + 41 = r2 ----- eq (iii)
h2 - 2h + k2 - 4k + 5 = r2 ----- eq (i)
h2 - 6h + k2 - 12k + 45 = r2 ----- eq (ii)
h2 - 10h + k2 - 8k + 41 = r2 ----- eq (iii)
4h + 8k - 40 = 0 ----- Subtracting eq (ii) from eq (i)
4h + 8k = 40
4(h + 2k) = 4(10)
h + 2k = 10 ---- eq (iv)
4h - 4k + 4 = 0 ----- Subtracting eq (iii) from eq (ii)
4h - 4k = - 4
4(h - k) = 4(- 1)
h - k = - 1 --- eq (v)
h + 2k = 10 ---- eq (iv)
h - k = - 1 --- eq (v)
3k = 11 ---- Subtracting eq (v) from eq (iv) ---- Substituting (5, 4) for (x, y)
25 - 10h + h2 + 16 - 8k + k2 = r2
h2 - 10h + k2 - 8k + 41 = r2 ----- eq (iii)
h2 - 2h + k2 - 4k + 5 = r2 ----- eq (i)
h2 - 6h + k2 - 12k + 45 = r2 ----- eq (ii)
h2 - 10h + k2 - 8k + 41 = r2 ----- eq (iii)
4h + 8k - 40 = 0 ----- Subtracting eq (ii) from eq (i)
4h + 8k = 40
4(h + 2k) = 4(10)
h + 2k = 10 ---- eq (iv)
4h - 4k + 4 = 0 ----- Subtracting eq (iii) from eq (ii)
4h - 4k = - 4
4(h - k) = 4(- 1)
h - k = - 1 --- eq (v)
h + 2k = 10 ---- eq (iv)
h - k = - 1 --- eq (v)
3k = 11 ---- Subtracting eq (v) from eq (iv)
 h -
h - 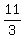 = - 1 ---- Substituting = - 1 ---- Substituting 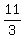 for k in eq (v) for k in eq (v)
 (x - h)2 + (y - k)2 = r2
(x - h)2 + (y - k)2 = r2
 -- Substituting (1, 2) for (x, y), and ( -- Substituting (1, 2) for (x, y), and (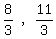 ) for (h, k) ) for (h, k)

 <==== Standard form of the equation of a CIRCLE <==== Standard form of the equation of a CIRCLE
 --- Substituting ( --- Substituting (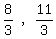 ) for (h, k), and ) for (h, k), and 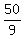 for r2 for r2
|
|
|
| |