|
Question 1208332: The car's speed decreased linearly as a function of time. The speed was 60 kph at t=1s and 40 kph at t = 5 s. Create a function that describes speed as a function of time. At what time did the car's speed equal 0?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
The car's speed decreased linearly as a function of time.
The speed was 60 kph at t=1s and 40 kph at t = 5 s.
Create a function that describes speed as a function of time. At what time did the car's speed equal 0?
~~~~~~~~~~~~~~~~~~~~~~~~
The function is
f(t) = V - at, (1)
where V is the initial speed at t= 0, "a" is the rate of the speed decreasing, t is the time (in seconds).
We don't know V at t= 0 (it is not given), but we can easily find "a".
"a" is the ratio of the change of the speed to the elapsed time
a = 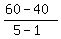 =  = 5 kilometer per hour per second.
Now from equation (1) we will find V
V - 5*1 = 60 ,
V = 60 + 5 = 65.
Thus the function is f(t) = 65 - 5t kilometers per hour. ANSWER
To find the stop time, write this equation
V = 65 - 5t = 0.
From the equation, t = 65/5 = 13 seconds from the beginning. ANSWER
Solved, with all necessary explanations.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
We are told that the speed as a function of time is linear, so let's use the standard notation for a linear function: y = mx+b where the dependent variable y is the car's speed and the independent variable x is the time in seconds.
In the standard form y=mx+b, m is the slope, or rate of change. In this problem, the speed decreased from 60kph to 40kph, a change of -20kph, in 4 seconds, between t=1 and t=5. So the slope m is -20/4 = -5.
So the linear function can now be written as y=-5x+b.
Use either of the two given data points to determine the value of b. The speed is 60 at t=1:
60 = -5(1)+b
60 = -5+b
b = 65
And now we have the full linear equation: y = -5x+65
Or, in formal function notation showing speed as a function of time...
ANSWER: s(t)=-5t+65
To find when the car's speed is 0, set s(t)=0 and solve.
-5t+65 = 0
5t = 65
t = 13
ANSWER: at 13 seconds
|
|
|
| |
