Question 1208291: Preliminary remark. This is an interesting question showing how, based on a mathematical model (the function B(t)) and partial data, one can then infer unknow properties of the modelled system. An important part of solving such questions is to translate properly the elements of information given in the text of the questions in mathematical terms, i.e. to figure out what is the equation to solve. Species are going extinct due to climate change at an unprecedented rate. If B(t) is the number of species (aka the Biodiversity) t years from now and B0 = B(0) is the current number of species then the equation for the B(t) is given by: B(t) = B0e^−at
A) if there are 200 species of animals in yellowstone national park in 2021 and 198 species next year (2022), what is the value of a?
ANSWER a= 0.01005
B)How long(how many years from 2021) do you expect it to be before there are only 100 species of animals in Yellowstone?
ANSWER 69.0 years
C) Assume that the Serengeti (a very large national park in the Eastern Africa country of Tanzania) is losing species at the same rate as Yellowstone National Park. If thirty years from now when your grandchild (if you have any) and you visit the Serengeti and you observe 100 species, how many species would you observe if you were to go there today?
Found 3 solutions by josgarithmetic, ikleyn, math_tutor2020:
Answer by josgarithmetic(39625)   (Show Source):
Answer by ikleyn(52850)  (Show Source):
You can put this solution on YOUR website! .
As usual at this forum, the solution, the numbers and the answer a = 0.713
in the post by @josgarithmetic are all incorrect (fatally wrong).
As usual in such cases, your humble servant (i.e. me) came to make the job
in a way how it SHOULD be done.
B(t) = 
 = 
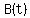--- (A) ---
That time length passage was 1 year.
 = 
 = 
= 
 = 
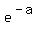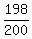
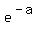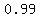
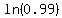
= -0.010050336.
Hence, a = 010050336, so the answer (a) in your post is correct.
--- (B) ---
For (b), we write this exponential equation
 = 100.
It is direct translation of words to Math.
From this equation, we should find time t, in years.
From the equation
 =  ,
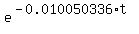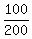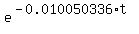=  = 0.5.
Take natural logarithm of both sides
-0.010050336*t = ln(0.5)
-0.010050336*t = -0.693147181
t = 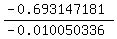 = 68.96756298.
We round it to the closest greater integer number of years, in order for the desire event happens.
ANSWER for (b) is 69 years.
Solved.
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
Part (a)
B(t) = B0*e^(-at)
B(t) = 200*e^(-at)
B(1) = 200*e^(-a*1)
198 = 200*e^(-a)
e^(-a) = 198/200
e^(-a) = 0.99
a = -Ln(0.99)
a = 0.01005 approximately when rounding to 5 decimal places.
--------------------------------------------------------------------------
Part (b)
B(t) = B0*e^(-at)
B(t) = 200*e^(-0.01005t)
100 = 200*e^(-0.01005t)
e^(-0.01005t) = 100/200
e^(-0.01005t) = 0.5
-0.01005t = Ln(0.5)
t = -Ln(0.5)/0.01005
t = 68.96986871243 approximately
t = 69 years when rounding to the nearest whole number.
Adding this duration to the year 2021 lands on the year 2021+69 = 2090.
--------------------------------------------------------------------------
Part (c)
B(t) = B0*e^(-at)
B(30) = B0*e^(-0.01005*30)
100 = B0*e^(-0.01005*30)
100 = B0*0.73971
B0 = 100/0.73971
B0 = 135.18811
B0 = 135
If 100 species will be observed in 2021+30 = 2051, then we estimate roughly 135 species were present in 2021.
Side note: I interpret the "now", from "If thirty years from now", to refer to when the problem was written (assuming 2021) rather than this current year (2024). The math professor who wrote this problem should be more careful in her/his wording.
|
|
|
