Question 1208264: Peter can mow a lawn in 40 minutes. John can mow the same lawn in 60 minutes. How long will it take them to mow the lawn together?
Found 4 solutions by ikleyn, josgarithmetic, math_tutor2020, greenestamps:
Answer by ikleyn(52756)   (Show Source):
You can put this solution on YOUR website! .
Peter can mow a lawn in 40 minutes. John can mow the same lawn in 60 minutes.
How long will it take them to mow the lawn together?
~~~~~~~~~~~~~~~~~~~
Peter makes 1/40 of the job per minute.
John makes 1/60 of the job per minute.
Working together, they make  +  =  +  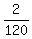=  =  of the job per minute.
Hence, they will complete the job in 24 minutes working together.
Solved without using any equations, easy and pleasantly with manipulating fractions only,
in a way accessible to any beginner student, using an appropriate logic and an adequate technique,
learning a necessary conception of the rate of work on the way
and without memorizing any formulas (which you will forget in the next 5 minutes).
------------------
It is a typical word problem on joint work.
To see many other similar (and different) problems on joint work,
solved with complete explanations to teach you, look into the lessons
- Using Fractions to solve word problems on joint work
- Solving more complicated word problems on joint work
- Selected joint-work word problems from the archive
Read them and get be trained in solving joint-work problems.
Consider these lessons as your textbook, handbook, guidebook, tutorials and (free of charge) home teacher,
which is always with you to help and to inspire.
//////////////////////
When a person comes to this forum with such problem, it clearly means that he/she
sees such problem for the first time and wants to be learned from scratch.
Learning from scratch, the only way to comprehend the method is to go through such conceptions
as the rate of work, to go through fractions and manipulating with fractions.
Any other method, if it does not teach you to these conceptions and does not teach you
manipulating with fractions, does not suit for the first time learning and is simply a waste of precious time.
It is just checked by teachers for centuries and does not require other justifications.
When you complete learning the basic method, you can look around for other approaches (but not vice versa).
To be sure that you learned the method enough, you should solve 3-5-10 different
problems of this kind on your own, using this technique/logic/reasoning.
Answer by josgarithmetic(39614)  (Show Source):
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
Answer: 24 minutes
Reason
Consider a 120 sq ft lawn.
I'm picking this value since it's the LCM of 40 and 60.
It turns out that this value doesn't matter.
This is because you can use any positive real number you want for the area, and you will arrive at the same answer.
Peter, when working alone, can mow the 120 sq ft lawn in 40 minutes.
His unit rate is 120/40 = 3 sq ft per minute.
rate = amountDone/time
On the other hand, if John works alone, then he takes 60 minutes.
John's unit rate is 120/60 = 2 sq ft per minute.
Let's now have them work together.
Doing so means they combine their unit rates to get 3+2 = 5 sq ft per minute.
This will assume neither worker hinders the other.
Then,
rate*time = amountDone
(5 sq ft per min)*(x minutes) = 120 sq ft
5x = 120
x = 120/5
x = 24 minutes is the amount of time needed if Peter and John work together.
Answer by greenestamps(13196)  (Show Source):
You can put this solution on YOUR website!
You have received solutions from other tutors showing a couple of different ways of solving this kind of problem. Here is another method.
Consider the least common multiple of the two given times, which is 120 minutes.
In 120 minutes, Peter could mow 120/40 = 3 of these lawns; in 120 minutes John could mow 120/60 = 2 of these lawns.
So together in 120 minutes the two of them could mow 3+2 = 5 of these lawns; and that means that together the two of them can mow the one lawn in 120/5 = 24 minutes.
This kind of problem (2 workers working together) is very common on tests in timed math competitions. For a shortcut to get you to the answer quickly without having to do formal algebra, the answer is
(product of the two times) divided by (sum of the two times)
For this problem: 
|
|
|
