Question 1208258: Hi, can you help me with part b please:
A particle is oscillating in Simple Harmonic Motion and is 𝑥 metres away from the origin after 𝑡 seconds. The movement of the particle can be modelled with the equation 𝑥 = 2 cos(3𝑡 + 𝛼)
a) Prove that its acceleration is −9𝑥 𝑚𝑠^-2.
b) If initially, 𝑥 = 1𝑚 with velocity 3√3 𝑚𝑠^-1, find a suitable value for 𝛼.
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Hi, can you help me with part b please:
A particle is oscillating in Simple Harmonic Motion and is 𝑥 metres away from the origin after 𝑡 seconds.
The movement of the particle can be modelled with the equation 𝑥 = 2 cos(3𝑡 + 𝛼)
a) Prove that its acceleration is −9𝑥 𝑚𝑠^-2.
b) If initially, 𝑥 = 1𝑚 with velocity 3√3 𝑚𝑠^-1, find a suitable value for 𝛼.
~~~~~~~~~~~~~~~~~~~
Since you ask about part (b) only, I will focus on it.
We are given that initially x= 1 m. The term "initially" means "at t= 0".
It gives this equation
2cos(a) = 1,
cos(a) =  ,
a =  or a =  . (1)
We also are given that "initially" velocity is  m/s.
Velocity is the first derivative of the position function with respect to time,
so this condition leads to this equation
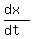 = at t= 0,
or
-2*3sin(3t+a) = at t= 0,
sin(3t+a) =  at t= 0,
or
sin(a) = .
a =  or a = . (2)
Comparing (1) and (2), we conclude that
a = .
At this point, the solution is complete and the answer is achieved.
ANSWER. A suitable value of "a" is a = .
Surely, you can add  to it, k = 0, +/-1, +/-2, . . . , if you want.
Solved, answered and explained.
|
|
|
