SOLUTION: The average price of an ostrich-skin underpants is $ 12,837. The prices are normally distributed with a standard deviation of $ 1500. If an ostrich-skin garment is picked randoml

Any normal distribution curve is a bell-shaped curve.

The probability that the price of an ostrich-skin garment is more than $15,000
is the area under the given normal curve to the right of the raw mark x= $15000. 


So, find the standard z-score for $15000, then use the standard normal distribution table 
to find the probability that a value is greater than that z-score.    


Step 1.  Find the z-score for 15000

             z = 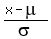 =  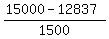 = 1.442. 


Step 2.  Use the standard normal distribution table to find the probability 
         that a value is greater than z = 1.442. 
         The table gives the probability  0.9251  that a value is less than a given z-score. 
         To find the probability that a value is greater than a given z-score, 
         subtract the probability from 1. 

             P(z > 1.44) = 1-P(z < 1.44)

             P(z > 1.44)= 1-0.9251 

             P(z > 1.44) = 0.0749.    ANSWER