SOLUTION: Hi David jogged for 5 days in a row. Each day he jogged 1.4km more than the day before. At the end of 5 days he jogged a total of 20.6km. How far did he jogged on the 5th day.

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Hi David jogged for 5 days in a row. Each day he jogged 1.4km more than the day before. At the end of 5 days he jogged a total of 20.6km. How far did he jogged on the 5th day.       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1208236: Hi
David jogged for 5 days in a row. Each day he jogged 1.4km more than the day before. At the end of 5 days he jogged a total of 20.6km. How far did he jogged on the 5th day.
Found 3 solutions by math_tutor2020, ikleyn, MathTherapy:
Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Answer: 6.92 km

Work Shown

x = amount jogged on day 1 only
x+1.4 = amount jogged on day 2 only
(x+1.4)+1.4 = x+2*1.4 = amount jogged on day 3 only
(x+2*1.4)+1.4 = x+3*1.4 = amount jogged on day 4 only
(x+3*1.4)+1.4 = x+4*1.4 = amount jogged on day 5 only

Add up the expressions mentioned.
Set the sum equal to 20.6 and solve for x.
day1+day2+day3+day4+day5 = total
x+(x+1.4)+(x+2*1.4)+(x+3*1.4)+(x+4*1.4) = 20.6
(x+x+x+x+x)+(1.4+2*1.4+3*1.4+4*1.4) = 20.6
5x+1.4(1+2+3+4) = 20.6
5x+1.4(10) = 20.6
5x+14 = 20.6
5x = 20.6-14
5x = 6.6
x = 6.6/5
x = 1.32
David jogged 1.32 km on day 1.
He jogged x+4*1.4 = 1.32+4*1.4 = 6.92 km on the 5th day.

Check:
day1 = 1.32 km
day2 = 1.32+1.4 = 2.72 km
day3 = 1.32+2*1.4 = 4.12 km (or 2.72+1.4 = 4.12)
day4 = 1.32+3*1.4 = 5.52 km (or 4.12+1.4 = 5.52)
day5 = 1.32+4*1.4 = 6.92 km (or 5.52+1.4 = 6.92)
total = 1.32+2.72+4.12+5.52+6.92 = 20.6
This checksum verifies we have the correct answer.


--------------------------------------------------------------------------

Another approach

We have an arithmetic sequence.
The first term is a1 = x.
The common difference is d = 1.4
Sn = sum of the first n terms
Sn = (n/2)*(2*a1+d*(n-1))
Sn = (n/2)*(2x+1.4(n-1))
Then plug n = 5 into this
S5 = (5/2)*(2x+1.4(5-1))

Set this equal to 20.6 and solve for x.
(5/2)*(2x+1.4(5-1)) = 20.6
2.5*(2x+5.6) = 20.6
5x+14 = 20.6
The steps to solving this are shown in the previous section.

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
David jogged for 5 days in a row. Each day he jogged 1.4km more than the day before.
At the end of 5 days he jogged a total of 20.6km. How far did he jogged on the 5th day.
~~~~~~~~~~~~~~~~~~~~~~


            Consider this simple way solving. 


The average distance, which David jogged per day, is 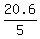 20.6%2F5 = 4.12 kilometers.


Intuitively, it is clear that this average distance is the distance which David jogged on the 3rd day

(3rd term is the central term of an arithmetic sequence of 5 terms).


From here, we conclude that on the 4th day David jogged 4.12 + 1.4 = 5.52 kilometers,

                            on the 5th day David jogged 5.52 + 1.4 = 6.92 kilometers.    ANSWER

Solved mentally without using any equations.


To me, the entire educational meaning of this problem for a student is to find a straightforward
simplest way to solve to the end, avoiding long boring calculations and long boring reasoning.

One brilliant idea dissects the problem and solves it instantly.



Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
Hi
David jogged for 5 days in a row. Each day he jogged 1.4km more than the day before. At the end of 5 days
he jogged a total of 20.6km. How far did he jogged on the 5th day. 

The MIDDLE day of the 5-day period is the matrix%281%2C6%2C+%285+%2B+1%29%2F2%2C+%22=%22%2C+6%2F2%2C+%22=%22%2C+3%5E%28rd%29%2C+day%29
On the MIDDLE or 3rd day, he jogged the AVERAGE/MEAN number of miles, or matrix%281%2C4%2C+20.6%2F5%2C+%22=%22%2C+4.12%2C+miles%29

He jogged 4.12 miles on the 3rd day, and consistently jogged 1.4 miles greater than previous days. 
So, on the 5th day (2 days after the 3rd day), he jogged 4.12 + 2(1.4) = 4.12 + 2.8 = 6.92 miles.

OR.

This is an AP/AS (Arithmetic Progression/Arithmetic Sequence) that the following SUM of an AP formula
can be used. matrix%281%2C3%2C+S%5Bn%5D%2C+%22=%22%2C+%28n%2F2%29%282a%5B1%5D+%2B+%28n+-+1%29d%29%29, with: Sn = Sum of the sequence (20.6, in this case)
                                               n = Number of terms (5,in this case)
                                              a1 = The 1st term of the sequence (UNKNOWN, in this case)
                                               d = Common difference (1.4, in this case)

          matrix%281%2C3%2C+20.6%2C+%22=%22%2C+%285%2F2%29%282a%5B1%5D+%2B+%285+-+1%291.4%29%29 ---- Substituting 20.6 for Sn, 5 for n, and 1.4 for d
          
           4.12 = a1 + 2.8
     4.12 - 2.8 = a1
           1.32 = a1 (First term of this AP/AS)

On the 5th day, he jogged 1.32 + (5 - 1)(1.4) = 1.32 + 4(1.4) = 1.32 + 5.6 = 6.92 miles.

To find the 5th term, you could've also used the following formula for a specific tern of an
AP/AS: matrix%281%2C3%2C+a%5Bn%5D%2C+%22=%22%2C+a%5B1%5D+%2B+%28n+-+1%29d%29, with: an = a Specific tern of the sequence (UNKNOWN, in this case)
                                  n = Term Number being sought (5, in this case)
                                 a1 = The 1st term of the sequence (1.32, in this case)
                                  d = This sequence's common difference (1.4, in this case)
SELAH!!