Question 1208213: if y = sin (t) , x = ln (t) , then ,(d ^2 y)/(dx ^2)=... when (x = π)
Found 3 solutions by math_tutor2020, ikleyn, mccravyedwin:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
x = ln(t)
t = e^x
y = sin(t)
y = sin(e^x)
First Derivative using Chain Rule.
y = sin(e^x)
dy/dx = cos(e^x)*d/dx[ e^x ]
dy/dx = cos(e^x)*e^x
Second Derivative using Product Rule and Chain Rule.
dy/dx = cos(e^x)*e^x
(d^2y)/(dx^2) = -sin(e^x)*e^x*e^x + cos(e^x)*e^x
(d^2y)/(dx^2) = e^x * ( cos(e^x) - sin(e^x)*e^x )
Evaluate at x = pi
(d^2y)/(dx^2) = e^x * ( cos(e^x) - sin(e^x)*e^x )
(d^2y)/(dx^2) = e^pi * ( cos(e^pi) - sin(e^pi)*e^pi )
(d^2y)/(dx^2) = 479.215377
The decimal value is approximate.
The calculator must be set to radian mode.
Answer by ikleyn(52914)  (Show Source):
You can put this solution on YOUR website! .
if y = sin (t) , x = ln (t) , then ,(d ^2 y)/(dx ^2)=... when (x = π)
~~~~~~~~~~~~~~~~~~~~~~~~
If x = ln(t), then
t =  , (1)
where "e" is the base of natural logarithms.
Therefore, in this problem, after making substitution (1), we have
y = sin(e^x), (2)
i.e. function y is expressed as the composition of function sine and exponent.
So, we apply the formula for the derivative of a composite function and find
first derivative of y with respect to x
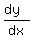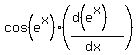 =  =  . (3)
Then we find second derivative as the derivative of (3)
d^2 y
------- (x) =  + =  + .
d^2 x
Now we substitute x =  to get
d^2 y
-------  =  +  .
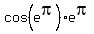d^2 x
To get the value, use in calculations approximate values e = 2.71828, pi = 3.14159.
d^2 y
------- =  +  .
d^2 x
With high precision online calculator WolframAlpha
https://www.wolframalpha.com/input?i=e%5Epi*cos%28e%5Epi%29-e%5E%282*pi%29*sin%28e%5Epi%29
the answer is this approximate value 479.215377365591689133.
Solved.
In this calculations, high accuracy regarding decimals is not required;
making correct formulas and showing understanding is just enough.
Answer by mccravyedwin(409)  (Show Source):
|
|
|
