Question 1208211: Good afternoon,
Please help me?
If there are 12 horses in a race what are the odds of selecting the exact finishing order of all 12 horses?
Could you please give me a formula to calculate any other odds also? As in, 10 horses, 7 horses or other numbers of horses.
Thank you in anticipation.
Regards
Faye
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
n = some positive integer = 1,2,3,...
If you had n horses then the general formula is: 1/(n!)
The exclamation mark indicates a factorial.
Factorials mean we start at the given integer and count down to 1.
Multiply along the way.
Examples:
12! = 12*11*10*9*8*7*6*5*4*3*2*1 = 479001600
10! = 10*9*8*7*6*5*4*3*2*1 = 3628800
If there are n = 12 horses, then 12! = 479001600 is the number of ways to arrange the 12 horses.
479001600 is roughly 479 million.
There's only one winning arrangement for any given horse race, which is why the answer as a fraction is 1/479001600
That fraction converts to the approximate decimal of 0.000000002088
There are 8 copies of "0" between the decimal point and the "2088".
--------------------------------------------------------------------------
A smaller example.
Let's say there are 3 horses.
Name them A,B,C.
There are n! = 3! = 3*2*1 = 6 ways to arrange them
The 6 arrangements are
ABC
ACB
BAC
BCA
CAB
CBA
Only one of these 6 arrangements will be the result of the race.
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Good afternoon,
Please help me?
If there are 12 horses in a race what are the odds of selecting the exact finishing order of all 12 horses?
Could you please give me a formula to calculate any other odds also?
As in, 10 horses, 7 horses or other numbers of horses.
Thank you in anticipation.
Regards
Faye
~~~~~~~~~~~~~~~~~~~~~~~~~
(a) 12 horses. Want to find the probability of guessing right order for all 12 horses.
In all, there are 12! = 12*11*10* . . . * 3*2*1 = 479001600 different finishing orders.
Of them, only one order is winning.
Therefore, the probability to guess the winning order is P =  = = 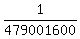 = 2.08768E-09,
which is very small number.
In terms of odds, the odds to guess the winning order correctly are 1 against 479001600-1 = 47900159.
(b) 12 horses. Want to find the probability of guessing right order for some particular 10 horses.
Again, there are 12! = 12*11*10* . . . * 3*2*1 = 479001600 different finishing orders.
Winning orders are those, where these particular 10 horses finish in the assigned order,
while 12-10 = 2 horses can finish in any arbitrary order among remaining positions.
So, the number of winning orders is 2! = 2 (two last horses finish in any order among remaining positions).
Therefore, the probability to guess the winning order is P = = 2.08768E-09,
which is very small number.
In terms of odds, the odds to guess the winning order correctly are 1 against 479001600-1 = 47900159.
(b) 12 horses. Want to find the probability of guessing right order for some particular 10 horses.
Again, there are 12! = 12*11*10* . . . * 3*2*1 = 479001600 different finishing orders.
Winning orders are those, where these particular 10 horses finish in the assigned order,
while 12-10 = 2 horses can finish in any arbitrary order among remaining positions.
So, the number of winning orders is 2! = 2 (two last horses finish in any order among remaining positions).
Therefore, the probability to guess the winning order is P =  = = 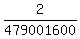 = 4.17535E-09,
which is also very small number.
In terms of odds, the odds to guess the winning order correctly are 2 against 479001600-2 = 47900158.
(c) 12 horses. Want to find the probability of guessing right order for some particular 7 horses.
Again, there are 12! = 12*11*10* . . . * 3*2*1 = 479001600 different finishing orders.
Winning orders are those, where these particular 7 horses finish in the assigned order,
while 12-7 = 5 horses can finish in any arbitrary order among remaining positions.
So, the number of winning orders is 5! = 5*4*3*2*1 = 120 (5 last horses finish in any order among remaining positions).
Therefore, the probability to guess the winning order is P = = 4.17535E-09,
which is also very small number.
In terms of odds, the odds to guess the winning order correctly are 2 against 479001600-2 = 47900158.
(c) 12 horses. Want to find the probability of guessing right order for some particular 7 horses.
Again, there are 12! = 12*11*10* . . . * 3*2*1 = 479001600 different finishing orders.
Winning orders are those, where these particular 7 horses finish in the assigned order,
while 12-7 = 5 horses can finish in any arbitrary order among remaining positions.
So, the number of winning orders is 5! = 5*4*3*2*1 = 120 (5 last horses finish in any order among remaining positions).
Therefore, the probability to guess the winning order is P = 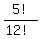 = = 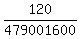 = 2.50521E-07,
which is still very small number.
In terms of odds, the odds to guess the winning order correctly are 120 against 479001600-120 = 479001480. = 2.50521E-07,
which is still very small number.
In terms of odds, the odds to guess the winning order correctly are 120 against 479001600-120 = 479001480.
Thus you have now standard templates on how to make reasoning and
how to calculate the probabilities and the odds in any other appropriate case.
|
|
|