Question 1208190: Let S={1,2,3,4,…,n}, and let A and B be two subsets of S such that A ≠ ∅, B ≠ S, and A ⊆ B.
Calculate the number of ordered pairs (A,B) for all subsets of the set S
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let S={1,2,3,4,…,n}, and let A and B be two subsets of S such that A ≠ ∅, B ≠ S, and A ⊆ B.
Calculate the number of ordered pairs (A,B) for all subsets of the set S.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Set S contains n distinguishable elements.
Let m be an integers number 0 <= m <= n.
The number of different subsets B in S, consisting of m elements, is  .
Notice that in this formula, I admit B = S. This case will be excluded later.
So, for given integer m between 1 and n, we can choose subset B in .
Notice that in this formula, I admit B = S. This case will be excluded later.
So, for given integer m between 1 and n, we can choose subset B in  different ways.
Let B is one such selected set of m elements.
The number of all different subsets A in B is different ways.
Let B is one such selected set of m elements.
The number of all different subsets A in B is 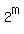 .
Notice that in this formula, I admit A = ∅. This case will be excluded later.
Having this, we conclude that the number of all pairs (A,B), where A is a subset in B, is the sum of products .
Notice that in this formula, I admit A = ∅. This case will be excluded later.
Having this, we conclude that the number of all pairs (A,B), where A is a subset in B, is the sum of products
 .
This sum is REMARCABLE. It is nothing else as .
This sum is REMARCABLE. It is nothing else as 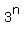 .
Indeed, this sum is a binomial expansion/decomposition of .
Indeed, this sum is a binomial expansion/decomposition of 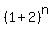 , which can be folded back , which can be folded back
 = = 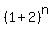 = = 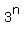 .
OK. It is the major idea and the major breakthrough. At this point, the problem is almost fully solved.
To fully complete the solution, we only need to exclude all pairs (A,B), where B = S or A = ∅.
The number of pairs (A,S) is the same as the number of all subsets A in S: it is .
OK. It is the major idea and the major breakthrough. At this point, the problem is almost fully solved.
To fully complete the solution, we only need to exclude all pairs (A,B), where B = S or A = ∅.
The number of pairs (A,S) is the same as the number of all subsets A in S: it is  , including subset (∅,S).
The number of pairs (∅,B) is the same as the number of subsets B in S: it is , including subset (∅,S).
The number of pairs (∅,B) is the same as the number of subsets B in S: it is  again, including subset (∅,S).
So, when we exclude the prohibited pairs, we will get
the number of all pairs under the problem's question is again, including subset (∅,S).
So, when we exclude the prohibited pairs, we will get
the number of all pairs under the problem's question is 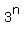 - -  - -  + 1 = + 1 = 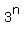 - - 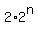 + 1.
I added 1 to compensate the fact that above I excluded the pair (∅,S) twice.
ANSWER. The number of all pairs under the problem's question is + 1.
I added 1 to compensate the fact that above I excluded the pair (∅,S) twice.
ANSWER. The number of all pairs under the problem's question is 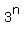 - - 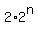 + 1. + 1.
Now the problem is solved completely.
Nice Math Olympiad level problem.
|
|
|