Question 1208186: Tickets for a raffle cost $18. There were 757 tickets sold. One ticket will be randomly selected as the winner, and that person wins $1900 and also the person is given back the cost of the ticket. For someone who buys a ticket, what is the Expected Value (the mean of the distribution)?
If the Expected Value is negative, be sure to include the "-" sign with the answer. Express the answer rounded to two decimal places.
Expected Value = $
Found 3 solutions by mccravyedwin, ikleyn, greenestamps:
Answer by mccravyedwin(408)   (Show Source):
You can put this solution on YOUR website!
Winnings Probability Expectations
--------------------------------------------------
1900+18 1/757 1918(1/757)= 2.533685601
-18 756/757 (-18)(756/757)=-17.97622193
--------------------------------------------------
Total expectation =-15.44253633
If the same lottery were held many times and 757 tickets
were sold every time, and you bought 1 ticket every time,
then by the time you'd have played about 757 times, you'd
have won about one time and you'd have averaged having
lost about $15.44 per game.
Answer = -$15.44
Edwin
Answer by ikleyn(52817)  (Show Source):
You can put this solution on YOUR website! .
Tickets for a raffle cost $18. There were 757 tickets sold. One ticket will be randomly selected
as the winner, and that person wins $1900 and also the person is given back the cost of the ticket.
For someone who buys a ticket, what is the Expected Value?
~~~~~~~~~~~~~~~~~~~~~~
The expected value of which distribution ?
In such problems, usually two different expected values sit in and are considered for a gamer.
One expected value is the expected value of winning for a gamer. It is
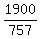 = 2.50990753 dollars.
In this specific problem, the winner pays $18 for his ticket, but then obtains
these $18 back, so we can do not count these mutually annihilate operations.
Regarding the winner and the winning ticket, in this problem we only need to count the winning amount of $1900.
Another expected value is the expected value of the game for a gamer.
In this problem, 756 tickets of 757 tickets lose $18 each, and one ticket of 757 tickets wins $1900.
So, the expected value of the game is
loosed winning final
tickets ticket expectation
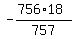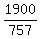 + = -15.4663144 dollars.
Since the problem does not concretize, which of the two possible expected values is of interest,
I make two conclusions from the post.
- First is that the problem, as it is worded, is posed incorrectly (it is incomplete).
- Second one is that the author does not know a subject,
does not know how the problem should be worded,
and is not sure to which of the two expected values his question goes.
In formulation of a mathematical problem, everything must be clean and clear.
----------------
In the post by @mccravyedwin, the logic of the solution and the final answer are incorrect.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
757 tickets were sold for $18 each; for the people running the lottery, the total income was 757($18) = $13626.
1 winning ticket was drawn, with a prize of $1900, and the $18 cost of the ticket was returned to the winner. For the people running the lottery, the total expenditures was $1900+$18 = $1918.
For the people running the lottery, the net gain was $13626-$1918 = $11708.
For the people running the lottery, the average gain per ticket sold was $11708/757 = $15.4663....
For the people buying the tickets, the average "gain" was -$15.4663....
ANSWER: -$15.4663....
|
|
|
