.
If f(x)= 1/((1/x)-3) , find the domain of f(f(x))
~~~~~~~~~~~~~~~~~~~~~~~~~~
In order for the function f(x) be defined, every occurred denominator should/must be different from zero.
So, we write f(x) = 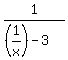 , and we see that
x must be different from 0: (x =/= 0);
and
, and we see that
x must be different from 0: (x =/= 0);
and
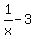 must be different from 0, which implies
must be different from 0, which implies
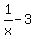 =/= 0, 1 =/= 3x, x =/= 1/3.
In this way, we obtain the first necessary condition:
function f(x) is defined over the set of all real numbers, except of x= 0 and/or x= 1/3.
+--------------------------------------------------+
| At this point, half of the problem is solved, |
| and the domain of f(x) is determined. |
| Now I will work to solve the second half, |
| which is finding the domain for f(f(x)). |
+--------------------------------------------------+
Now, in order for f(f(x)) be defined, these two additional conditions must be satisfied:
f(x) =/= 0 and f(x) =/= 1/3.
If f(x) is defined, then f(x) =
=/= 0, 1 =/= 3x, x =/= 1/3.
In this way, we obtain the first necessary condition:
function f(x) is defined over the set of all real numbers, except of x= 0 and/or x= 1/3.
+--------------------------------------------------+
| At this point, half of the problem is solved, |
| and the domain of f(x) is determined. |
| Now I will work to solve the second half, |
| which is finding the domain for f(f(x)). |
+--------------------------------------------------+
Now, in order for f(f(x)) be defined, these two additional conditions must be satisfied:
f(x) =/= 0 and f(x) =/= 1/3.
If f(x) is defined, then f(x) = 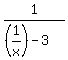 =
= 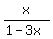 .
Since x= 0 is not in the domain, we see that if f(x) is defined, then it is never equal to zero;
so this case is over without giving new restrictions.
If f(x) is defined and f(x) = 1/3, then
.
Since x= 0 is not in the domain, we see that if f(x) is defined, then it is never equal to zero;
so this case is over without giving new restrictions.
If f(x) is defined and f(x) = 1/3, then
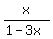 =
=  ,
3x = 1 - 3x ---> 3x + 3x = 1 ---> 6x = 1 ---> x = 1/6.
Thus, the domain of f(f(x)) is the set of all real numbers except of 0, 1/3 and 1/6.
Now the problem is solved completely.
ANSWER. The domain of f(f(x)) is the set of all real numbers except of 0, 1/3 and 1/6.
,
3x = 1 - 3x ---> 3x + 3x = 1 ---> 6x = 1 ---> x = 1/6.
Thus, the domain of f(f(x)) is the set of all real numbers except of 0, 1/3 and 1/6.
Now the problem is solved completely.
ANSWER. The domain of f(f(x)) is the set of all real numbers except of 0, 1/3 and 1/6.
Solved completely.