Question 1208178: Hi
Bob bought a pair of shoes. He also spent 1/4 of the remainder of his money on a pair of pants. He had $189 left. If the cost of the pants was 3/7 the cost of the shoes, what is the price of the shoes.
Found 4 solutions by math_tutor2020, ikleyn, greenestamps, MathTherapy:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Answer: $147
Work Shown
x = starting amount of money
y = price of the shoes
x-y = amount remaining after buying the shoes
(1/4) of (x-y) = (x-y)/4 = amount spent on pants
(3/4) of (x-y) = 3(x-y)/4 = final amount left = 189
3(x-y)/4 = 189
x-y = (4/3)*189
x-y = 252
We'll use this equation in the next section.
pants = (3/7)*shoes
(x-y)/4 = (3/7)*y
7(x-y) = 4*3y
7*(x-y) = 12y
7*(252) = 12y ....... replace x-y with 252
y = 7*252/12
y = 147 is the cost of the shoes.
Let's find x.
x-y = 252
x-147 = 252
x = 252+147
x = 399
Bob started with $399.
Check:
x-y = 399-147 = 252 is the amount remaining after buying the shoes
252/4 = 63 is the cost of the pants
start-shoes-pants = 399-147-63 = 189 is the final amount remaining after buying the shoes and pants.
Since we arrive at the 189 mentioned in the instructions, it helps us confirm that we got the correct dollar amounts.
Answer by ikleyn(52788)  (Show Source):
You can put this solution on YOUR website! .
Bob bought a pair of shoes. He also spent 1/4 of the remainder of his money on a pair of pants.
He had $189 left. If the cost of the pants was 3/7 the cost of the shoes, what is the price of the shoes.
~~~~~~~~~~~~~~~~~~~~~
To avoid denominators, let 3x be the cost of the pair of pants.
Then the cost of the pair of shoes is 7x, according to the problem.
Let T be the total of money Bob had originally.
Then for the total we have this equation
T = 3x + 7x + 189. (1)
The remainder after buying the pair of shoes is (T-7x).
From the problem, we have this equation
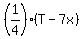 = 3x. (2) (Bob spent 1/4 of the remainder of his money on a pair of pants)
Thus we have two equations, (1) and (2), for two unknowns x and T.
From equation (1),
T = 10x + 189. (3)
From equation (2),
T - 7x = 12x,
or
T = 12x + 7x = 19x. (4)
Now we substitute T = 19x from (4) into (3). We get
19x = 10x + 189,
19x - 10x = 189
9x = 189
x = 189/9 = 21.
Now we are in position to find the cost of the pair of shoes. It is 7x = 7*21 = 147 dollars. ANSWER
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Presumably a solution using formal algebra was desired; you have received two responses with very different formal solutions.
But you can get very good mental exercise (and problem-solving experience) by solving the problem less formally, using logical reasoning and simple arithmetic.
Bob had $189 left after spending 1/4 of his remaining money on a pair of pants. That means the $189 was 3/4 of his remaining money. 1/4 is one-third of 3/4, so the amount he spent on the pants was 1/3 of $189, or $63.
The cost of the pants was 3/7 of the cost of the shoes, so the cost of the shoes was 7/3 of the cost of the pants. So the cost of the shoes was (7/3)*$63 = 7*$21 = $147.
ANSWER: $147
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Hi
Bob bought a pair of shoes. He also spent 1/4 of the remainder of his money on a pair of pants. He had $189 left. If the cost of the pants was 3/7 the cost of the shoes, what is the price of the shoes.
Let the amount he started with, and cost of shoes, be A and S, respectively
After buying the shoes, he had A - S left
Amount spent on pants: 
Amount remaining after purchase of pants: 
Since $189 remained after purchase of pants, we get: 
 ------ Canceling GCF, 3, in numerators
Since cost of pants is 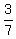 the cost of the shoes (S), so we get: 
 ----- Substituting 63 for 
3S = 7(63) --- Cross-multiplying
Cost of shoes, or 
|
|
|
