Question 1208177: Hi
Mr Thomas spent $1972 on cars and dolls. He bought 3 times as many cars as dolls. Each doll cost $10 more than each car. She paid $476 more for the cars than the dolls. What is the cost of a doll.
Found 5 solutions by ikleyn, greenestamps, mccravyedwin, josgarithmetic, MathTherapy:
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
Mr Thomas spent $1972 on cars and dolls. He bought 3 times as many cars as dolls.
Each doll cost $10 more than each car. She paid $476 more for the cars than the dolls.
What is the cost of a doll.
~~~~~~~~~~~~~~~~~~~
How Mr. Thomas suddenly became "She" ?
If it was an "artificial intelligence", who created this problem,
hence, this artificial intelligence has a defective logic inside, which should be fixed.
In order for do not scare people around.
Another version is that a professor who composed this problem was drunk.
Third version is that the problem's creator does not read what he/she writes and posts.
Appropriate problem to submit it for shNobel prize competition.
//////////////////////////
From the problem, we know that the total cost was $1972, and the cost for the cars
was $476 more than for the dolls.
Hence, the cost for the cars was 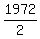 +  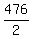= 1224 dollars,
and the cost for the dolls was 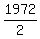- 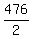= 748 dollars.
Let the number of the dolls be x.
Then the number of cars is 3x.
The price for one doll (each doll) is  .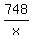
The price for one car (each car) is  =  .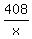
From the problem, we have this equation for the price difference
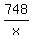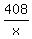- = 10 dollars.
Simplify and find x
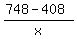 = 10
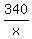 = 10
x = 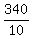 = 34.
Hence, the cost of a doll is  = 22 dollars. ANSWER
Solved.
Simply, easy, fresh and funny. And educative.
Answer by greenestamps(13214)  (Show Source):
Answer by mccravyedwin(409)  (Show Source):
You can put this solution on YOUR website!
Take advantage of available technology.
Use a separate letter for every unknown,
which makes setting up a problem easy.
Let the number of cars = c
Let the cost of a car = x
Let the number of dolls = d
Let the cost of a doll = y
Mr. Thomas spent $1972 on cars and dolls.
cx + dy = 1972
He bought 3 times as many cars as dolls.
c = 3d
Each doll cost $10 more than each car.
y = x + 10
She paid $476 more for the cars than the dolls.
Cx = Dy + 476
What is the cost of a doll?
Go to this site:
https://www.emathhelp.net/en/calculators/algebra-2/system-of-equations-solver/?
Where it says "Enter a system of equations, type in
cx + dy = 1972, c = 3d, y = x + 10, cx = dy + 476
Click "calculate".
Scroll down and read
c = 102, d = 34, x = 12, y = 22
Cost of a doll = $y = $22
Edwin
Answer by josgarithmetic(39630)  (Show Source):
Answer by MathTherapy(10557)  (Show Source):
You can put this solution on YOUR website!
Hi
Mr Thomas spent $1972 on cars and dolls. He bought 3 times as many cars as dolls. Each doll cost $10 more than each car. She paid $476 more for the cars than the dolls. What is the cost of a doll.
Let cost of ALL dolls purchased be x
Since $476 MORE was spent on cars than dolls, then amount spent on cars was x + 476
Since a total of $1,972 was spent, we get: x + x + 476 = 1,972
2x = 1,972 - 476
2x = 1,496
Cost of ALL dolls, or 
So, cost of ALL cars = 1,972 - 748 = $1,224
Let price of each doll, be D
Then price of each car = D - 10
Number of dolls purchased: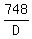 
Number of cars purchased: 
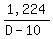Since he bought 3 times as many cars as dolls, we get the following
NUMBER-OF-ITEMS equation: 
 --- Canceling GCF, 12, in numerators
102D = 187(D - 10) --- Cross-multiplying
102D = 187D - 1,870
102D - 187D = - 1,870
- 85D = - 1,870
Cost of each doll, or 
|
|
|
