Question 1208127: A right triangle has one vertex on the graph of y = 9 - x^2, x > 0 at (x,y) another at the origin, and the third on the positive x-axis at (x,0). Express the area A of the triangle as a function of x.
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A right triangle has one vertex on the graph of y = 9 - x^2, x > 0 at (x,y) another at the origin,
and the third on the positive x-axis at (x,0). Express the area A of the triangle as a function of x.
~~~~~~~~~~~~~~
Three given points are (0,0) (the origin), (x,0) and (x,9-x^2) with x > 0.
They form a right-angled triangle with the right angle at x-axis.
Notice that 2 cases are possible.
(1) 0 < x < 3. Then the triangle is in quadrant I.
(2) 3 < x <  . Then the triangle is in quadrant IV.
In any case, the legs of this triangle are x units and |9-x^2| units (absolute value).
At x= 3 the triangle is degenerated; so it is a special case,
which does not fit to the problem's formulation.
So, the area of this triangle is A(x) = . Then the triangle is in quadrant IV.
In any case, the legs of this triangle are x units and |9-x^2| units (absolute value).
At x= 3 the triangle is degenerated; so it is a special case,
which does not fit to the problem's formulation.
So, the area of this triangle is A(x) = 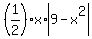 , x > 0, x =/= 3. ANSWER , x > 0, x =/= 3. ANSWER
Solved.
|
|
|