Question 1208105: Hi
The tennis club and badminton club have a total of 109 members. The number of boys in the tennis club is 6/11 the members of this club. The number of girls in the badminton club is 4/9 the members of this club. How many boys are there in both clubs.
Found 3 solutions by ikleyn, EPMcCravy, greenestamps:
Answer by ikleyn(52782)   (Show Source):
You can put this solution on YOUR website! .
The tennis club and badminton club have a total of 109 members.
The number of boys in the tennis club is 6/11 the members of this club.
The number of girls in the badminton club is 4/9 the members of this club.
How many boys are there in both clubs.
~~~~~~~~~~~~~~~~~~~~~~
From the condition, in the tennis club, there are 6x boys and 5x girls,
where x is some counting number, now unknown;
in the badminton club, there are 5y boys and 4y girls,
where y is some (possibly, another) counting number, now unknown.
For these numbers, x and y, we have this equation
(6x+5x) + (5y+4y) = 109, (1)
or
11x + 9y = 109. (2)
We should solve it in integer positive numbers.
From this equation, we write
y = 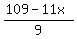 (3)
and we are looking to find such x from the set of integers [1,9] that y in formula (3) be integer.
Making "trials and errors", we find the unique solution
x= 5, y= 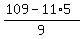 =  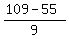=  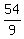= 6.
ANSWER. The total number of boys in both clubs is 6x + 5y = 6*5 + 5*6 = 60.
Solved.
On the way, I explained to you how to solve Diophantine equation (2) in integer positive numbers.
Notice that we managed to solve a problem with only one equation in two unknowns.
It was possible because the other restriction was that the solution must be in integer (whole) numbers.
Answer by EPMcCravy(4)  (Show Source):
You can put this solution on YOUR website!
Use capital letters B and G for boys and girls in the tennis club and
small letters b and g for boys and girls in the badminton club.
The tennis club and badminton club have a total of 109 members.
B + G + b + g = 109
The number of boys in the tennis club is 6/11 the members of this club.
B = (6/11)(B + G)
The number of girls in the badminton club is 4/9 the members of this club.
g = (4/9)(b + g)
How many boys are there in both clubs.
Go to https://www.wolframalpha.com/
type in B + G + b + g = 109, B = (6/11)(B + G), g = (4/9)(b + g)
For "integer solution", read
b = 55n + 30, B = 30 - 54n, g = 44n + 24, G = 25 - 45n, n element Z
Then since they must all be non-negative, choose n = 0
b = 30, B = 30, g = 24, G = 25
Add the boys, B + b = 30 + 30 = 60
Edwin
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Note that, grammatically, the question is stated incorrectly. "How many boys are there in both clubs?" means how many boys are in both the tennis club and the badminton club. There is no information given that allows us to answer that.
Clearly, the intent of the question is to ask for the total number of boys in the two clubs.
Working with that....
The boys in the tennis club are 6/11 of the total number of members, so there are 6x boys and 5x girls.
The girls in the badminton club are 4/9 of the total number of members, so there are 4y girls and 5y boys.
The total number of members in the two clubs is 109:
This is a Diophantine equation -- a single equation in two unknowns that has a finite number of solutions because of the restriction that both unknowns are positive integers.
To find the set of solutions, solve the equation for one unknown in terms of the other and use the fact that both unknowns are positive integers.
To make it easier to find the solution(s), perform the division as quotient plus remainder:
x is an integer, so 12-x is an integer; and y must be an integer. That means (1-2x)/9 must be an integer.
One solution is with x=5, which gives us 
So we have the solution x=5 and y=6; to look for other solutions, we can go back to the original equation and see that we can get other solutions by increasing x by 9 and decreasing y by 11, or by decreasing x by 9 and increasing y by 11. But neither of those gives us solutions in positive integers, so the solution we have is the unique solution.
The total number of boys in the two clubs is 6x+5y = 6(5)+5(6) = 30+30 = 60.
ANSWER: 60
|
|
|
