Question 1208069: what is the possible values of x in 2sin^2(x-30)=cos 60
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source):
You can put this solution on YOUR website! .
what  are the possible values of x in 2sin^2(x-30)=cos 60
~~~~~~~~~~~~~~~~~~~~~
They want you find all real solutions to this equation
2sin^2(x-30) = cos(60). (1)
We have
cos(60) = 1/2; so, this equation takes the form
2sin^2(x-30) = 1/2.
Simplify it step by step
sin^2(x-30) = 1/4,
sin(x-30) = +/- },
sin(x-30) = +/- 1/2. (2)
From this equation, there are two infinite sets of roots for x-30 to equation (2)
x-30 = 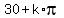 , k = 0, +/-1, +/-2, . . .
x-30 = 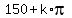 , k = 0, +/-1, +/-2, . . .
It gives two infinite sets of roots for x to equation (1)
x = 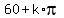 , k = 0, +/-1, +/-2, . . .
x =  , k = 0, +/-1, +/-2, . . .
ANSWER. Equation (1) has two infinite sets of solutions
x = 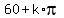, k = 0, +/-1, +/-2, . . .
x = , k = 0, +/-1, +/-2, . . .
Solved.
======================
To tutor @greenestamps and to all other readers of this post.
Thank you for your attention, but my solution, as it is/was written by me
from the very beginning, is correct and includes all the cases sin(x-30) = +/- 1/2.
It is because the general formula uses not full period  , but half period  , which absorbs/covers all these cases.
So, everything is and was correct in my post. There is no reason to worry.
This alarm from @greenestamps is false.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
For tutor @ikleyn....
Currently your post only shows solutions for sin(x-30) = 1/2; you left out the solutions for sin(x-30) = -1/2
|
|
|
