Question 1208063: The area of △ABC is 40. Points P, Q and R lie on sides AB, BC and CA respectively. If AP = 3 and PB = 5, and the area of △ABQ is equal to the area of PBQR, determine the area of △AQC?
Found 6 solutions by ikleyn, Edwin McCravy, AnlytcPhil, mccravyedwin, Plocharczyk, EPMcCravy:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The area of △ABC is 40. Points P, Q and R lie on sides AB, BC and CA respectively.
If AP = 3 and PB = 5, and the area of △ABQ is equal to the area of PBQR, determine the area of △AQC.
~~~~~~~~~~~~~~~~~~~~
It looks like I made an error in my reasoning/solution.
Thanks to Edwin for noticing it.
I think that there is no sense to keep that wrong solution here, so I delete it.
If I will have some other ideas, I will place them here.
Thanks to Edwin again.
Sorry for inconvenience.
\\\\\\\\\\\\\ August 20, 2024, approximately one week later \\\\\\\\\\\\\\\
It took some time for me to find another - correct - solution,
but finally I found it and place this my updated solution below.
\\\\\\\\\\\\\\\\\\ August 20, 2024 \\\\\\\\\\\\\\\\\\\\
.
The area of △ABC is 40. Points P, Q and R lie on sides AB, BC and CA respectively.
If AP = 3 and PB = 5, and the area of △ABQ is equal to the area of PBQR, determine the area of △AQC.
Solution
This problem is very nice.
It is nice, because the major idea of the solution is hidden -
it is not on the surface and should be dug up.
Due to this reason, it is a typical Math Olympiad problem.
Before to move forward, make a sketch of the problem.
I will assume that the sketch is in front of your eyes.
Let O be the intersection point of PR and AQ.
Let  be the angle ∠AOP = ∠QOR : be the angle ∠AOP = ∠QOR :  = ∠AOP = ∠QOR
(these angles are congruent since they are vertical angles).
Since the areas of triangle ABQ and quadrilateral PBQR are equal, we conclude from this fact
that the areas of triangles AOP and ROQ are equal. The equation for these equal areas is = ∠AOP = ∠QOR
(these angles are congruent since they are vertical angles).
Since the areas of triangle ABQ and quadrilateral PBQR are equal, we conclude from this fact
that the areas of triangles AOP and ROQ are equal. The equation for these equal areas is
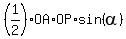 = =  . (1)
After reducing, from (1) we have
OA*OP = OQ*OR. (2)
It leads to proportion . (1)
After reducing, from (1) we have
OA*OP = OQ*OR. (2)
It leads to proportion
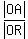 = = 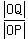 . (3)
Thus we see that triangles AOR and QOP have congruent angles AOR and QOP and proportional sides
that conclude these angles. So, these triangles AOR and QOP are SIMILAR.
It is the key idea of the solution.
What follows, is the direct consequence of this idea.
So, the triangles AOR and QOP are similar.
From it, we conclude that these triangles have congruent corresponding angles.
In particular, angles OAR and OQP are congruent.
It implies that line AR is parallel to PQ.
It is the same as to say that PQ is parallel to AC.
Hence, triangle PBQ is similar to triangle ABC.
From this similarity, we have . (3)
Thus we see that triangles AOR and QOP have congruent angles AOR and QOP and proportional sides
that conclude these angles. So, these triangles AOR and QOP are SIMILAR.
It is the key idea of the solution.
What follows, is the direct consequence of this idea.
So, the triangles AOR and QOP are similar.
From it, we conclude that these triangles have congruent corresponding angles.
In particular, angles OAR and OQP are congruent.
It implies that line AR is parallel to PQ.
It is the same as to say that PQ is parallel to AC.
Hence, triangle PBQ is similar to triangle ABC.
From this similarity, we have 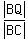 = =  = = 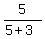 = = 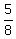 .
Thus we proved that under given condition, point Q divides the side BC in the same proportion .
Thus we proved that under given condition, point Q divides the side BC in the same proportion 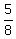 as the point P divides side AB.
Hence, the area of triangle AQC is
as the point P divides side AB.
Hence, the area of triangle AQC is  of the area of triangle ABC, i.e. of the area of triangle ABC, i.e.  = 3*5 = 15 square units.
At this point, the problem is solved completely. = 3*5 = 15 square units.
At this point, the problem is solved completely.
Nice ( ! )
\\\\\\\\\\\\\\\\\\\\\\ Sept.18,2024 \\\\\\\\\\\\\\\\\\\\\\\\\\\\\
As I said at the beginning, this solution is the fixed version of my previous incorrect solution.
Edwin's notes relate to that previous, now outdated solution,
which I just deleted and replaced by this updated CORRECT version.
So, Edwin's notes do not relate to this last solution and are not relevant to it anymore.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There is a fallacy in Ikleyn's proof above. I will draw just enough of it to
show the fallacy. While she is correct that triangles AOP and QOR are
congruent, QR is not necessarily parallel to AP, and therefore not necessarily
parallel to AB as she has stated. I do not see that she has proved it parallel.
We must rule out the possibility of the figure on the right below, and show that
the figure on the left is the correct one. She is correct that QR = AP = 3, but
she must show that QR is parallel to AP. I think she can show this by making
use of the fact that QR = 3 and the converse of this well-known theorem:
If a line parallel to one side of a triangle intersects the other two sides,
then it divides the two sides proportionally. (The converse is also true.)
If Ikleyn will correct this error in her proof, I will delete this post. So that
the student will learn of the corrected proof, I will make another post in
one of my other screen names, to inform him or her of the correction.
  Below I have drawn the figure for the whole problem, but I purposely drew QR to
look not quite parallel to AB, which Ikleyn will prove it to be. She is welcome
to use my figure below.
Below I have drawn the figure for the whole problem, but I purposely drew QR to
look not quite parallel to AB, which Ikleyn will prove it to be. She is welcome
to use my figure below.
 Edwin
Edwin
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website!
After thinking about it, maybe it isn't necessary to prove QR is parallel to AP,
but only that the areas of those two triangles are equal. Each would add the
same amount of area to quadrilateral PBQO. I just noticed that QR was not proved
parallel to AP, though it was stated that they were parallel. It would also be
interesting to prove that they are parallel. That might be more of a challenge
than the original problem.
Edwin
Answer by mccravyedwin(408)   (Show Source): (Show Source):
You can put this solution on YOUR website!
But after thinking about it some more, it is necessary to prove QR is parallel
to AP, for if QR and AP weren't parallel, then triangles RQC and ABC would not be
similar. So while it wouldn't matter to get the area of triangle ABQ equal to the
area of quadrilateral PBQR, it is absolutely necessary to determine the area of
triangle AQC. We'll see what Ikleyn can do about proving them parallel. I now
think it's necessary.
Edwin
Answer by Plocharczyk(17)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn is too much like Trump. She can't stand to be wrong. But she is.
She has not proved QR is parallel to AB. And that is absolutely necessary to
determine the area of AQC. Sure, she got the right answer, but the question
is to prove it, not get it!
She did not show that angles OAP and QAR are congruent. Just because the product
of two sides are equal, does not show which way the triangles are turned.
Edwin
Answer by EPMcCravy(4)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn, I'm going to show you your error.
 Let O be the intersection point of PR and AQ.
Let
Let O be the intersection point of PR and AQ.
Let  be the angle AOP = QOR : be the angle AOP = QOR :  = AOP = QOR
(these angles are congruent since they are vertical angles).
So far, so good.
Since the areas of triangle ABQ and quadrilateral PBQR are equal, we conclude from this fact
that the areas of triangles AOP and ROQ are equal. The equation for these equal areas is = AOP = QOR
(these angles are congruent since they are vertical angles).
So far, so good.
Since the areas of triangle ABQ and quadrilateral PBQR are equal, we conclude from this fact
that the areas of triangles AOP and ROQ are equal. The equation for these equal areas is
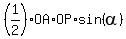 = =  . (1)
So far, so good. That's the SAS area formula. . (1)
So far, so good. That's the SAS area formula.
  After reducing, from (1) we have
OA*OP = OQ*OR. (2)
So far, so good! But be aware that is true for both cases above, not for just
the one on the left.
It leads to proportion
After reducing, from (1) we have
OA*OP = OQ*OR. (2)
So far, so good! But be aware that is true for both cases above, not for just
the one on the left.
It leads to proportion
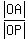 = = 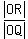 . (3)
So far, so good! But I repeat, that is also true for both cases above, not for
just the one on the left.
Thus we see that triangles AOP and QOR have congruent angles AOP and QOR and proportional sides
that conclude these angles. So, these triangles AOP and QOR are SIMILAR.
So far, so good. But I'm still warning you, that is also true for both cases.
above, not for just the one on the left.
So, the triangles AOP and QOR are similar.
From it, we conclude that these triangles have congruent corresponding angles.
That is also true for both cases above, not for just the one on the left.
In particular, angles OAP and OQR are congruent.
AHA!!! There is your fallacy right there!!! You cannot assume that!!!!!
It could be angles OAP and ORQ that are congruent.
See, Ikleyn? We all make mistakes. Are you saying that this is not a mistake?
You know very well it is! I apologize for getting angry. But proofs are either
valid or not. If a proof is not valid, no amount of whining or trashing me will
make it valid. You must prove that AP and QR are parallel. You have not done that.
Why not admit that you can make mistakes?
Edwin . (3)
So far, so good! But I repeat, that is also true for both cases above, not for
just the one on the left.
Thus we see that triangles AOP and QOR have congruent angles AOP and QOR and proportional sides
that conclude these angles. So, these triangles AOP and QOR are SIMILAR.
So far, so good. But I'm still warning you, that is also true for both cases.
above, not for just the one on the left.
So, the triangles AOP and QOR are similar.
From it, we conclude that these triangles have congruent corresponding angles.
That is also true for both cases above, not for just the one on the left.
In particular, angles OAP and OQR are congruent.
AHA!!! There is your fallacy right there!!! You cannot assume that!!!!!
It could be angles OAP and ORQ that are congruent.
See, Ikleyn? We all make mistakes. Are you saying that this is not a mistake?
You know very well it is! I apologize for getting angry. But proofs are either
valid or not. If a proof is not valid, no amount of whining or trashing me will
make it valid. You must prove that AP and QR are parallel. You have not done that.
Why not admit that you can make mistakes?
Edwin
|
|
|