SOLUTION: For each point (a,b) that is on the graph of y = f(x), the point (2a +1, 3b) is plotted, forming the graph of another function y = g(x). As an example, the point (0,2) lies on the

This type of problem requires knowing how to shift graphs right and 
left, stretching and shrinking, both horizontally and vertically.
It is also necessary that the transformations are done in the right
order, multiplications first then additions and subtractions.

Vertical transformations are done to the function itself, the whole
"right side".

Vertical transformations are as they seem, adding and subtracting
to shift up and down, multiplying by factors > 1 to stretch, 
multiplying by factors < 1 to shrink.
  
Horizontal transformation are done to x.

Horizontal transformation are "backward" from what they seem, adding
to x to shift left, subtracting from x to shift right, multiplying
by the reciprocal of factors > 1 to stretch, and multiplying by 
factors > 1 to shrink.

Since the x-value of f(x) is 'a' and the x-value on g(x) is '2a+1',
the factor of 2 in '2a+1' means that the graph of f(x) is stretched 
horizontally by a factor of 2, which means we multiply x by the
reciprocal of 2, which is 1/2. 

So doing only that horizontal stretch would give us 

Then the term +1 in '2a+1' means that we shift the graph right by 1 unit,
which means we subtract 1 from x or, add -1 to x

so doing that would give us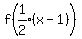 

That finishes doing everything required to do to the x-coordinate.

Now the 3 factor in "3b" means that the graph is stretched vertically by
a factor of 3, so we multiply the entire function by 3.

That gives us 

So the answer is



Edwin

(b)  As the problem describes, we start from the point (a,b) = (a,f(a)).
     
     We transform it into the point (2a+1,g) = (2a+1,3f(a)).


     So,  g(2a+1) = 3*f(a).    (1)


     Now we want to call 2a+1 as new variable x;  so we write

           x = 2a + 1,  which means that  a = .

  
     Then the equality (1) takes the form

            g(x) = 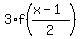.    (2)


     This formula (2) defines function g(x) via function f(x).

      So, formula (2) is the answer to question (b).


      At this point, part (b) is complete.



(c)  Based on formula (2) from part (b), the transformations that can be applied to the graph of y = f(x) 
     to obtain the graph of y = g(x)  are as follows:


         - shift the plot of f(x) 1 unit right;

         - then stretch x-axis with coefficient 2;

         - then stretch y-axis with coefficient 3.

Manipulations are hard to understand without visual interpretations.
Here is a visual illustration of this problem with the
case 

We begin with 




Then we stretched it horizontally by a factor of 2,
giving us the graph of

 



Then we shifted it right 1 unit, giving us the graph of

 



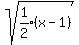
Then finally we stretched the graph vertically by a factor
of 3, giving us the final graph of 



So 

Here are the graphs of f(x) and g(x), the red one is f(x),
and the blue graph is g(x).



The point (4,2) lies on the graph of y = f(x), so the point (2•4+1, 3•2),
or (9,6) lies on the graph of y = g(x)

Edwin