Question 1208027: Find the valee of k and the 17 term of each of the following arithmetic sequence
6)2k+1,5k-3, 7k-2
7) 7k+2,5k+4,4k-5
Found 2 solutions by mccravyedwin, ikleyn:
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the  value of k and the value of k and the  17-th term of each of the following arithmetic sequence 17-th term of each of the following arithmetic sequence
6) 2k+1,5k-3, 7k-2
7) 7k+2,5k+4,4k-5
~~~~~~~~~~~~~~~~~~~~~~~~~
I will solve first part, leaving the second part to you as an exercise,
because the second part is a TWIN to the first part.
Since three terms  , ,  and and  form an arithmetic progression,
the difference form an arithmetic progression,
the difference 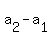 is the same as the difference is the same as the difference 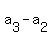 (as each this difference is simply d, the common difference of the AP).
So, we write
(5k-3) - (2k+1) = (7k-2) - (5k-3).
From this equation, we find the value of k
5k - 3 - 2k - 1 = 7k - 2 - 5k + 3,
3k - 4 = 2k +1
3k - 2k = 1 + 4
k = 5.
Now we know the value of k and can restore the values of the first three twrms of this AP
(as each this difference is simply d, the common difference of the AP).
So, we write
(5k-3) - (2k+1) = (7k-2) - (5k-3).
From this equation, we find the value of k
5k - 3 - 2k - 1 = 7k - 2 - 5k + 3,
3k - 4 = 2k +1
3k - 2k = 1 + 4
k = 5.
Now we know the value of k and can restore the values of the first three twrms of this AP
 = 2*5+1 = 11; = 2*5+1 = 11;
 = 5*5-3 = 22; = 5*5-3 = 22;
 = 7*5-2 = 33.
Thus, the progression has first term 11 and the common difference d = 22-11 = 11.
At this point, we know everything about this AP and can easily find each of its terms.
In particular, the 17-th term of this AP is = 7*5-2 = 33.
Thus, the progression has first term 11 and the common difference d = 22-11 = 11.
At this point, we know everything about this AP and can easily find each of its terms.
In particular, the 17-th term of this AP is  = =  + d*(n-1) = 11 + 11*(17-1) = 11 + 11*16 = 187. ANSWER + d*(n-1) = 11 + 11*(17-1) = 11 + 11*16 = 187. ANSWER
Solved.
This solution is your TEMPLATE to solve many other similar problems.
In particular, the other part is a TWIN and can be solved by the same way.
Literally follow my solution, step by step.
You may report me about your progress.
|
|
|