SOLUTION: if f (x) = 1/(1 - x) , then (f(f(f(f...f)(sqrt2),(45 times) = ...., A) 0, B)(2 - sqrt2)/2, C)(2 + sqrt2)/2, D) 1, E) sqrt2

Algebra ->  Complex Numbers Imaginary Numbers Solvers and Lesson -> SOLUTION: if f (x) = 1/(1 - x) , then (f(f(f(f...f)(sqrt2),(45 times) = ...., A) 0, B)(2 - sqrt2)/2, C)(2 + sqrt2)/2, D) 1, E) sqrt2      Log On


   

Question 1208001: if f (x) = 1/(1 - x) , then (f(f(f(f...f)(sqrt2),(45 times) = ...., A) 0, B)(2 - sqrt2)/2, C)(2 + sqrt2)/2, D) 1, E) sqrt2
Found 2 solutions by mccravyedwin, ikleyn:
Answer by mccravyedwin(408) About Me  (Show Source):
You can put this solution on YOUR website!
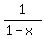
f%28x%29%22%22=%22%221%2F%281-x%29

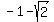
f%28sqrt%282%29%29%22%22=%22%221%2F%281-sqrt%282%29%29, rationalizing the denominator gives -1-sqrt%282%29

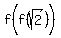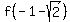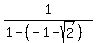f%28f%28sqrt%282%29%29%5E%22%22%29f%28-1-sqrt%282%29%29%22%22=%22%221%2F%281-%28-1-sqrt%282%29%29%29, simplifying and rationalizing the denominator gives %282-sqrt%282%29%29%2F2

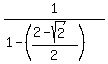f+%28+f%28+f%28sqrt%282%29%5E%22%22%29%5E%22%22+%29%5E%22%22+%29+%29%22%22=%22%221%2F%281-%28%282-sqrt%282%29%29%2F2%29%29, simplifying and rationalizing the denominator gives sqrt%282%29

And we're back where we started, at sqrt%282%29

So we conclude:

When there are 0 f's, the answer is sqrt%282%29
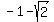When there is 1 f, the answer is -1-sqrt%282%29
When there are 2 f's, the answer is %282-sqrt%282%29%29%2F2
When there are 3 f's, the answer is sqrt%282%29
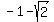When there is 4 f's, the answer is -1-sqrt%282%29
When there are 5 f's, the answer is %282-sqrt%282%29%29%2F2
When there are 6 f's, the answer is sqrt%282%29

It keeps cycling around through those 3 values.

So we conclude that when there is a multiple of 3 f's, the
answer is sqrt%282%29

Since 45 is a multiple of 3, the answer is sqrt%282%29.

Edwin

Answer by ikleyn(52852) About Me  (Show Source):
You can put this solution on YOUR website!
.
If f (x) = 1/(1 - x) , then (f(f(f(f...f)(sqrt2),(45 times) = ....,
A) 0,
B) (2 - sqrt2)/2,
C) (2 + sqrt2)/2,
D) 1,
E) sqrt2.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

If f(x) = 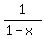1%2F%281-x%29,  


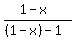then  f(f(x)) = 1%2F%281-1%2F%281-x%29%29 = %281-x%29%2F%28%281-x%29-1%29 = %28x-1%29%2Fx,


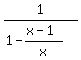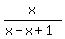then  f(f(f(x))) = 1%2F%281-%28x-1%29%2Fx%29 = x%2F%28x-x%2B1%29 = x.


Thus, applying function f to any real number x =/= 1,  x =/= 0  three times, we get x again.



In other words,  f(f(f(x))) == x identically, for all real x =/= 1,  x =/= 0.



So, for example,  f%28f%28f%28sqrt%282%29%29%29%29 = sqrt%282%29;  f%28f%28f%28sqrt%283%29%29%29%29 = sqrt%283%29;  f%28f%28f%28sqrt%285%29%29%29%29 = sqrt%285%29;  f%28f%28f%28sqrt%287%29%29%29%29 = sqrt%287%29;  

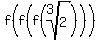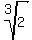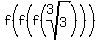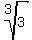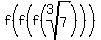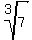                  f%28f%28f%28root%283%2C2%29%29%29%29 = root%283%2C2%29;  f%28f%28f%28root%283%2C3%29%29%29%29 = root%283%2C3%29;  f%28f%28f%28root%283%2C5%29%29%29%29 = root%283%2C5%29;  f%28f%28f%28root%283%2C7%29%29%29%29 = root%283%2C7%29,  and so on.



Since 45 is a multiple of 3,  f applied to  sqrt%282%29  45 times is  sqrt%282%29;

                              f applied to  sqrt%283%29  45 times is  sqrt%283%29;

                              f applied to  sqrt%285%29  45 times is  sqrt%285%29;

                              f applied to  sqrt%287%29  45 times is  sqrt%287%29;


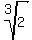                              f applied to  root%283%2C2%29  45 times is  root%283%2C2%29%29;

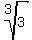                              f applied to  root%283%2C3%29  45 times is  root%283%2C3%29%29;

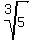                              f applied to  root%283%2C5%29  45 times is  root%283%2C5%29%29;

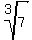                              f applied to  root%283%2C7%29  45 times is  root%283%2C7%29%29,

and so on.

Solved and significantly expanded.


For example,  f applied  2025  times to the number 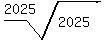 root%282025%2C2025%29%29  is  root%282025%2C2025%29.


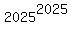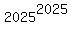Similarly,  f  applied  2025  times to the number  2025%5E2025  is  2025%5E2025.


As well as  f  applied  2025  times to the number  2025!  is  2025! , again.


You can easily construct a million other examples.