Question 1207940: The tangent line to a circle may be defined as the line that intersects the circle in a single point, called the point of tangency. If the equation of the circle is x^2 + y^2 = r^2 and the equation of the tangent line is y = mx + b, show that:
A. r^2(1 + m^2) = b^2
B. The point of tangency is [(-r^2 m)/b, (r^2/b)]
C. The tangent line is perpendicular to the line containing the center of the circle and point of tangency.
Found 2 solutions by Edwin McCravy, mananth:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We find the x-intercept of y = mx + b, by setting y = 0.
y = mx + b
0 = mx + b
-b = mx

 All 6 triangles ACO, AOB, OCB, ACO, ADC, DOC are similar, because a perpendicular
drawn from the right angle to the hypotenuse divides a right triangle into
two right triangles, each similar to it.
All 6 triangles ACO, AOB, OCB, ACO, ADC, DOC are similar, because a perpendicular
drawn from the right angle to the hypotenuse divides a right triangle into
two right triangles, each similar to it.




 And by the Pythagorean theorem:
And by the Pythagorean theorem:

 So equating expressions for BC2
So equating expressions for BC2


 ----------------------
For the coordinates of the point of tangency, C.
By similar triangles,
----------------------
For the coordinates of the point of tangency, C.
By similar triangles,


 <--the x-coordinate of the point of tangency C <--the x-coordinate of the point of tangency C


 <--the y-coordinate of the point of tangency C
So the point of tangency C is <--the y-coordinate of the point of tangency C
So the point of tangency C is 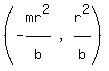 Edwin
Edwin
Answer by mananth(16946)   (Show Source): (Show Source):
|
|
|