Question 1207918: For A and B, find the standard form of the equation of each circle.
A. Center (1,0) and has the point (-3,2).
B. Center (-3,1) and tangent to the y-axis.
Found 3 solutions by mananth, MathTherapy, timofer:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! A
iven:
• Center: (1,0)
• Point on the circle: (−3,2)
We find the radius r by the distance between the center and the given point by the distance formula:
r=sqrt((x2−x1)^2+(y2−y1)^2)
Substitute the given coordinates
r=sqrt((−3)−1)^2+(2−0)^2)
r = sqrt(20)
r= 2 sqrt(5)
Equation of circle
(x-1)^2+ (y-0)^2 = (2sqrt(5))^2
(x-1)^2+y^2= 20 ---------------------------A
Given: center (−3,1)
Tangent to the y-axis
Since the circle is tangent to the y-axis, the radius r is the horizontal distance from the center to the y-axis. The x-coordinate of the center is −3
so the radius 𝑟 =3
(x−(−3)) ^2 +(y−1) ^2 = 3^2=9
(x+3)^2 +(y-1)^2 = 9
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
For A and B, find the standard form of the equation of each circle.
A. Center (1,0) and has the point (-3,2).
B. Center (-3,1) and tangent to the y-axis.
Standard form of the equation of a circle:  , where:  is a point on the circle's circumference
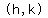 is the CENTER of the circle
 is the circle's RADIUS
 ----- Substituting (- 3, 2) for (x, y), and (1, 0) for (h, k)
<==== Standard form of the equation of a circle
 ----- Substituting (1, 0) for (h, k), and 20 for r2
 <=== Standard form of the equation of the circle with center (1,0) and point (-3,2) on its circumference
Answer by timofer(104)  (Show Source):
|
|
|
