Question 1207812: A picnic basket can hold a maximum of 30 apples and 20 sandwiches. Each apple takes up 1 unit of space, and each sandwich takes up 2 units of space. The picnic basket has a total capacity of 60 units of space. What is the maximum number of apples (x) and sandwiches (y) that can be packed?( This is a graphing question so if you read this do you think you could email me and I will send you the pictures of the questions o have 3 questions and if it’s necessary I am willing to pay for it.) Thank you i need the constraints,objetive function, Vertices of possible max./min, solutions, and of course the solution and graph ! Thank you so much ( This is a graphing question so if you read this do you think you could email me and I will send you the pictures of the questions o have 3 questions and if it’s necessary I am willing to pay for it.) Thank you i need the constraints,objetive function, Vertices of possible max./min, solutions, and of course the solution and graph ! Thank you so much
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
Answer by ikleyn(52855)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A picnic basket can hold a maximum of 30 apples and 20 sandwiches.
Each apple takes up 1 unit of space, and each sandwich takes up 2 units of space.
The picnic basket has a total capacity of 60 units of space.
What is the maximum number of apples (x) and sandwiches (y) that can be packed?
( This is a graphing question so if you read this do you think you could email me and I will send you the pictures of the questions o have 3 questions and if it’s necessary I am willing to pay for it.) Thank you i need the constraints,objetive function, Vertices of possible max./min, solutions, and of course the solution and graph ! Thank you so much ( This is a graphing question so if you read this do you think you could email me and I will send you the pictures of the questions o have 3 questions and if it’s necessary I am willing to pay for it.) Thank you i need the constraints,objetive function, Vertices of possible max./min, solutions, and of course the solution and graph ! Thank you so much
~~~~~~~~~~~~~~~~~~~~~
I will solve it using different method, applying logical reasoning and common sense.
I will not make any plots to save my time.
We want maximize the number of apples and sandwiches (more precisely, the sum of them),
satisfying the other given constraints.
Let's apply the most aggressive strategy.
We will take as much apples as possible (30 apples), since they take only 1 unit of space, each.
Then we complement it with appropriate number of sandwiches, which is
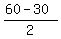 = 15 (the remaining space divided by 2).
So, the solution is 30 apples and 15 sandwiches, which gives the total of 30 + 15 = 45 items.
Notice that this solution satisfies all the constraints. = 15 (the remaining space divided by 2).
So, the solution is 30 apples and 15 sandwiches, which gives the total of 30 + 15 = 45 items.
Notice that this solution satisfies all the constraints.
Thus we solved the problem easy and elegantly using logical reasoning and common sense.
No plots are needed.
---------------
Outwardly, this problem is similar to Linear Programming problems,
where the geometric solution method is often used.
But concretely, this particular problem can be easily solved in MUCH SIMPLER WAY
using simple logic without any plots. That's why I call such tasks False Linear Programming problems.
All of your other today's problems belong to the same class/type,
and can be solved using logic, ONLY.
In my view, this simple logical solution is much more valuable solution method for the given problem
than to apply heavy artillery of the Linear Programming method blindly and without necessity.
|
|
|