|
Question 1207799: I have been answering textbook math questions for over 20 years. It is terribly embarrassing for me to admit that in all those years solving word problems have been a nightmare. I am sure most students agree that the wording is word problems are not always clear and precise.
Here is one:
Two pumps of different sizes, working together, can empty a fuel tank in 5 hours.The larger pump can empty this tank in 4 hours less than the smaller one. If the larger pump is out of order, how long will it take the smaller one to do the job alone?
Together two pumps can do the job in 5 hours.
I understand this:
Pump 1 + pump 2 = 5 hours.
Is this right?
Smaller pump = x
Larger pump = x - 4
Is this right?
Honestly, I now find myself guessing my way to an equation.
Here it is:
(1/x) + 1/(x - 4) = 5
If my equation and reasoning is wrong, explain why it is wrong.
Thanks
Found 5 solutions by greenestamps, timofer, MathTherapy, mccravyedwin, ikleyn:
Answer by greenestamps(13195)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Together two pumps can do the job in 5 hours.
I understand this:
Pump 1 + pump 2 = 5 hours.
Is this right?
We don't know what it means, so perhaps we don't know if it is right.
But in fact we know it can't be right, because the equation literally says the sum of two things is some number of hours. If you are adding two things and the sum is some number of hours, then the two things you are adding must be hours. Pumps are not hours.
Smaller pump = x
Larger pump = x - 4
Is this right?
Again we don't know, because we don't know what it means. Are "x" and "x-4" the names of the two pumps? I doubt it.
No matter how much experience you have working math problems, you are always potentially in trouble if you don't start with clear and precise definitions of the variables and expressions you are going to use.
The standard method for solving "working together" problems is to write an equation that says the sum of the fractions of the job that each worker does in some amount of time is equal to the fraction of the job that they do together in that time.
The problem says that the larger pump can do the job in 4 hours less than the smaller pump. So the proper definitions of "x" and "x-4" are
Let x = # of hours the smaller pump takes to do the job alone
Then x-4 = # of hours the larger pump takes to do the job alone
(Compare that to the "definitions" you show for x and x-4....)
Next, from there (as you tried to do in your setup),
Then 1/x = fraction of job done by smaller pump in 1 hour
And 1/(x-4) = fraction of job done by larger pump in 1 hour
Our equation is going to say "fraction done by one pump in 1 hour, plus fraction done by other pump in 1 hour, equals fraction done together in 1 hour". Since they can do the job together in 5 hours, the fraction of the job they do together in 1 hour is 1/5.
So, finally,

That completes the setup. Actually solving that leads to a very ugly quadratic equation, so I would use a tool like a graphing calculator to find the answer.
But perhaps what you were looking for was help in doing the setup....
Answer by timofer(104)   (Show Source): (Show Source):
You can put this solution on YOUR website! large pump rate 1/(x-4)
small pump rate one tank in uknown time, 1/x
both pumps combined 1/(x-4)+1/x=1/5, because when both tanks are working at the same
time, their rates are summed. This equation shows the described, 1 tank in 5 hours.
The property of adding in any order means also can say 1/x+1/(x-4)=1/5
Answer by MathTherapy(10549)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I have been answering textbook math questions for over 20 years. It is terribly embarrassing for me to admit that in all those years solving word problems have been a nightmare. I am sure most students agree that the wording is word problems are not always clear and precise.
Here is one:
Two pumps of different sizes, working together, can empty a fuel tank in 5 hours.The larger pump can empty this tank in 4 hours less than the smaller one. If the larger pump is out of order, how long will it take the smaller one to do the job alone?
Together two pumps can do the job in 5 hours.
I understand this:
Pump 1 + pump 2 = 5 hours.
Is this right?
Smaller pump = x
Larger pump = x - 4
Is this right?
Honestly, I now find myself guessing my way to an equation.
Here it is:
(1/x) + 1/(x - 4) = 5
If my equation and reasoning is wrong, explain why it is wrong.
Thanks
NOT QUITE!
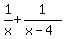 , the 2 COMBINED/SUMMED hourly-rates of the pumps, is correct.
However, both pumps working together, can empty the tank in 5 hours, or , the 2 COMBINED/SUMMED hourly-rates of the pumps, is correct.
However, both pumps working together, can empty the tank in 5 hours, or  of the tank in 1 hour
So, we get: of the tank in 1 hour
So, we get:  , and NOT: , and NOT: 
Answer by mccravyedwin(405)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Word problems having more than 1 unknown are easier to set up using a
separate letter for each unknown, and a separate equation for each
sentence. They are not necessarily easier to solve that way, but they're
easier to set up that way.
Look at the first sentence: Two pumps of different sizes, working together, can empty a fuel tank in 5 hours.If you write the equation first in words, it's pretty easy to see that that
sentence translates into this equation:
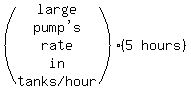     Suppose it takes the large pump L hours to empty the tank.
Then the large pump's rate is
Suppose it takes the large pump L hours to empty the tank.
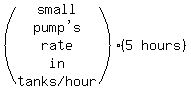
Then the large pump's rate is 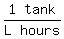 Suppose it takes the small pump S hours to empty the tank.
Then the small pump's rate is
Suppose it takes the small pump S hours to empty the tank.
Then the small pump's rate is 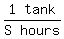 [Notice that S will be the final answer!]
So now we have this for the first sentence's equation:
[Notice that S will be the final answer!]
So now we have this for the first sentence's equation:
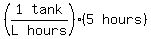  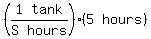   Taking out the words, we just have the equation.
Taking out the words, we just have the equation.
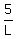     Now we look at the second sentence:
Now we look at the second sentence: The larger pump can empty this tank in 4 hours less than the smaller one.That is simply
     or, removing the words,
or, removing the words,
     So now you have two equations in 2 unknowns:
So now you have two equations in 2 unknowns:
 Then you just substitute S-4 for L in the first equation and you have
Then you just substitute S-4 for L in the first equation and you have
 Multiply through by LCD S(S-4)
Multiply through by LCD S(S-4)












 Those values are approximately, using the +, 12.4 hours and
using the -, 1.6 hours, and certainly we reject the second one,
so the answer is
Those values are approximately, using the +, 12.4 hours and
using the -, 1.6 hours, and certainly we reject the second one,
so the answer is 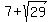 , approximately 12.385 hours.
Edwin , approximately 12.385 hours.
Edwin
Answer by ikleyn(52748)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In opposite to your lamentations about word problems, this concrete word problem in your post
is absolutely clear standard school Math problem, and it is written in a classic clear Math language.
Every word is correct, all the words are in their proper places, no excessive words
and all the words are connected in the right order, expressing very clear description and idea.
Every time, when Math problem is written by a professional, it is clear.
As a rule, such problems are brilliant pieces of art.
Many of them were developed and polished during hundreds of years,
in different countries and in different cultures
by people who cared about the mathematical education of subsequent generations.
If a wording Math problem is not clear, it means (with the probability of 129% ),
that the problem is written by a non-professional.
If somebody does not understand clearly written Math problems, it only means
that this person has no enough adequate training in solving/understanding such problems.
It doesn't mean anything else.
Those who have enough adequate training in solving Math problems, write the standard setup equation
immediately and without errors - - - because they are trained.
By the way, it is a simple criterion if the student
knows the subject in the school elementary Math.
The necessary and sufficient condition is that the student
writes the setup equation immediately and without errors.
|
|
|
| |