Question 1207787: The intensity I (in candlepower) of a certain light source obeys the equation I = 900/(x^2) , where x is the distance (in meters) from the light. Over what range of distances can an object be placed from this light source so that the range of intensity of light is from 1600 to 3600 candlepower, inclusive?
To find the range, I must evaluate the given equation for I by letting x = 1600 and then x = 3600.
Yes?
Answer by ikleyn(52810)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To find the range in the distance x, you should solve this compound inequality
1600 <= 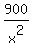 <= 3600.
+--------------------------------------+
| It is opposite to your intention, |
| as you presented it in your post. |
+--------------------------------------+
Left side of this inequality, 1600 <= <= 3600.
+--------------------------------------+
| It is opposite to your intention, |
| as you presented it in your post. |
+--------------------------------------+
Left side of this inequality, 1600 <= 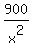 , gives you , gives you
 <= <= 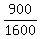 , ,  <= <=  , x <= , x <=  , x <= , x <=  = 0.75 meters.
Right side of this inequality, = 0.75 meters.
Right side of this inequality, 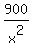 <= 3600, gives you <= 3600, gives you
 >= >=  , ,  >= >= 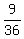 , x >= , x >= 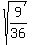 , x >= , x >=  = 0.5 meters.
Thus the ANSWER for the range of x is 0.5 meters <= x <= 0.75 meters. = 0.5 meters.
Thus the ANSWER for the range of x is 0.5 meters <= x <= 0.75 meters.
Solved in full, with complete explanation.
|
|
|