Question 1207779: Let z and w be complex numbers such that |z| = |w| = 1 and zw is not equal to -1.
(a) Prove that conjugate {z} = 1/z and conjugate{w} = 1/w
(b) Prove that ={z + w}/{zw + 1} is a real number.
Found 3 solutions by ikleyn, mccravyedwin, Edwin McCravy:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let z and w be complex numbers such that |z| = |w| = 1 and zw is not equal to -1.
(a) Prove that conjugate {z} = 1/z and conjugate{w} = 1/w
(b) Prove that ={z + w}/{zw + 1} is a real number.
~~~~~~~~~~~~~~~~~~~~~~~
Proof for part (a)
It is well known fact that the product  . .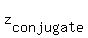 = |z|^2.
Indeed, if z = a + bi, then = |z|^2.
Indeed, if z = a + bi, then 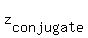 = a - bi, and, therefore, = a - bi, and, therefore,
 . .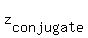 = (a+bi)*(a-bi) = = (a+bi)*(a-bi) =  = = 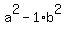 = =  = = 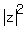 .
But we are given that |z| = 1; hence, .
But we are given that |z| = 1; hence, 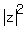 = 1.
Thus = 1.
Thus  . .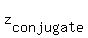 = 1.
Hence, = 1.
Hence, 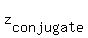 = =  .
It is what was required to prove.
For .
It is what was required to prove.
For 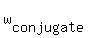 = = 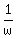 the proof is the same.
It is, actually, the same statement as the proof is the same.
It is, actually, the same statement as 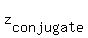 = =  , but expressed using letter w instead of z. , but expressed using letter w instead of z.
At this point, proof for part (a) is complete.
Proof for part (b)
z and w are unit complex numbers, in the sense that their modules are equal to 1 (given).
Hence, in geometric presentation in complex plane, z and w are adjacent side of a rhombus.
Then, according to the parallelogram rule of adding complex numbers, the sum z+w
is the diagonal of the rhombus on side z and w.
According to properties of a rhombus, its diagonal is a bisector of the angle
between vectors z and w.
Therefore, for the argument of the complex number z+w we can write
arg(z+w) = 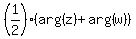 mod mod  . (1)
Now consider complex number zw. As the product of two complex unit numbers, it is a unit
complex number, too, i.e. has the modulus 1, and its argument is the sum of arguments z and w
arg(zw) = arg(z) + arg(w) mod . (1)
Now consider complex number zw. As the product of two complex unit numbers, it is a unit
complex number, too, i.e. has the modulus 1, and its argument is the sum of arguments z and w
arg(zw) = arg(z) + arg(w) mod  . (2)
Also, notice that "1" is a complex unit number too, with the argument arg(1) = 0.
Applying the same proof as in (1), we get
arg(zw+1) = . (2)
Also, notice that "1" is a complex unit number too, with the argument arg(1) = 0.
Applying the same proof as in (1), we get
arg(zw+1) =  = = 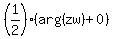 = =  mod mod  . (3)
Using (2), we can continue line (3) this way
arg(zw+1) = . (3)
Using (2), we can continue line (3) this way
arg(zw+1) = 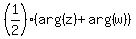 mod mod  . (4)
Comparing (1) with (4), we see that
arg(z+w) = arg(zw+1) mod . (4)
Comparing (1) with (4), we see that
arg(z+w) = arg(zw+1) mod  .
It means that complex numbers z+w and (zw+1) are either co-directed vectors or oppositely directed vectors.
In any case, it implies that the number .
It means that complex numbers z+w and (zw+1) are either co-directed vectors or oppositely directed vectors.
In any case, it implies that the number 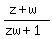 has the argument 0 or has the argument 0 or  mod mod  ,
i.e. is a real number.
At this point, the proof (b) is complete. ,
i.e. is a real number.
At this point, the proof (b) is complete.
Solved, proved and completed, in full.
Answer by mccravyedwin(407)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here's another way to do the (a) part:
Since |z| = |w| = 1
This problem is about points on the unit circle, where the horizontal axis
is the real axis and the vertical axis is the imaginary axis.
 All complex numbers on the unit circle have modulus 1., the radius of the
unit circle.
The conjugate of any complex number on the unit circle is obviously its
reflection in the horizontal (real) axis. It is also obvious that the
argument (angle) of the conjugate is the negative of the argument (angle).
The reciprocal of any complex number is that complex number when multiplied by
the complex number, gives the result 1, which is the complex number 1+0i,
thought of as the point (1,0).
DeMoivre's theorem tell us that to multiply two complex numbers, we
multiply their moduli and add their arguments.
So when we multiply the arguments of any two complex numbers on the unit circle,
we'll get 1.
It's also obvious to see that when you add the arguments, the
red and green arcs above, you will get 0 for the argument.
So it's obvious that the reciprocal and conjugate of any complex number of the
unit circle are the same.
This is what the (a) part asks you to prove:
We can write z and w in trigonometric form:
All complex numbers on the unit circle have modulus 1., the radius of the
unit circle.
The conjugate of any complex number on the unit circle is obviously its
reflection in the horizontal (real) axis. It is also obvious that the
argument (angle) of the conjugate is the negative of the argument (angle).
The reciprocal of any complex number is that complex number when multiplied by
the complex number, gives the result 1, which is the complex number 1+0i,
thought of as the point (1,0).
DeMoivre's theorem tell us that to multiply two complex numbers, we
multiply their moduli and add their arguments.
So when we multiply the arguments of any two complex numbers on the unit circle,
we'll get 1.
It's also obvious to see that when you add the arguments, the
red and green arcs above, you will get 0 for the argument.
So it's obvious that the reciprocal and conjugate of any complex number of the
unit circle are the same.
This is what the (a) part asks you to prove:
We can write z and w in trigonometric form:
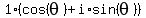
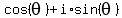 We will show that the reciprocal equals the conjugate:
We will show that the reciprocal equals the conjugate:
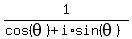
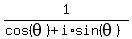  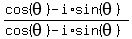
 Since the denominator equals 1,
Since the denominator equals 1,
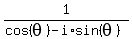  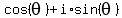 So the reciprocal of a complex number on the unit circle is also its
conjugate.
Edwin
So the reciprocal of a complex number on the unit circle is also its
conjugate.
Edwin
|
|
|