Question 1207746: Two cars enter the Florida Turnpike at Commercial Boulevard at 8:00 AM, each heading for Wildwood.One car’s average speed is 10 miles per hour more than the other’s.The faster car arrives at Wildwood at 11:00 AM, (1/2) hour before the other car.What was the average speed of each car? How far did each travel?
Found 4 solutions by mccravyedwin, MathTherapy, greenestamps, josgarithmetic:
Answer by mccravyedwin(408)   (Show Source):
You can put this solution on YOUR website!
One car’s average speed is 10 miles per hour more than the other’s.
So, during each of the 3 hours between 8AM and 11AM, The faster car gained an
additional 10 miles lead over the slower car.
So when the faster car arrived at his destination (in Wildwood), the slower car
was still (10)(3) = 30 miles behind.
It then took the slower car 1/2 hour to go those 30 miles.
Since the slower car went 30 miles in 1/2 hour, it could have gone 60 miles in 1
whole hour, so the slower car averaged 60 mph.
Therefore, the faster car averaged 60+10=70 mph.
So in 3 hours the faster car went (70)(3) = 210 miles.
Answers:
The slower car averaged 60 mph.
The faster car averaged 70 mph.
Each traveled 210 miles.
Now I'll let the other tutors put some algebra in the solution. For mine's too
"arithmeticky".
Edwin
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website!
Two cars enter the Florida Turnpike at Commercial Boulevard at 8:00 AM, each heading for Wildwood.One car’s average speed is 10 miles per hour more than the other’s.The faster car arrives at Wildwood at 11:00 AM, (1/2) hour before the other car.What was the average speed of each car? How far did each travel?
Let distance each traveled (from Commercial Blvd to Wildwood), be D
Let average speed of faster car, in mph, be S
Then average speed of slower car, in mph, is S - 10
Time faster car took to travel the distance: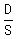 
Also, faster car took 3 hours (8:00 a.m. - 11:00 a.m.) to reach Wildwood
Then, faster car’s TIME equation is: 
D = 3S ------ eq (i)
Time slower car took to travel the distance,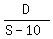 
And, slower car took 3½ hrs (½ hr more than faster car, or from 8:00 a.m. - 11:30 a.m.) to reach Wildwood
Slower car’s TIME equation is then: 
2D = 7(S - 10) --- Cross-multiplying
2D = 7S - 70 ----- eq (ii)
2(3S) = 7S - 70 ----- Substituting 3S for D in eq (ii)
6S = 7S - 70
6S - 7S = - 70
- S = - 70
Average speed of faster car, or 
Average speed of slower car: S - 10 = 70 - 10 = 60 mph
Distance traveled (Commercial Blvd to Wildwood): 3S = 3(70) = 210 miles
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Here is another non-algebraic way to solve the problem quickly and easily.
The faster car finished the trip in 3 hours; the slower car finished in 3.5 hours.
Since the distances are the same and the ratio of times is 3/3.5=6/7, the ratio of speeds is 7/6.
Since the ratio of speed is 7/6 and the difference in speeds is 10mph, the two speeds are 70mph and 60mph.
(You can reach that conclusion by observation and simple logical reasoning, or you can do it more formally using a proportion.)
ANSWERS:
speed of faster car: 70mph
speed of slower car: 60mph
distance each car traveled: 70(3)=210 miles, or 60(3.5)=210 miles
Answer by josgarithmetic(39625)  (Show Source):
|
|
|
