Question 1207741: If each coded item in a catalog begins with 3 distinct letters followed by 4 distinct nonzero digits, find the probability of randomly selecting one of these coded items with the first letter a vowel and the last digit even.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
If each coded item in a catalog begins with 3 distinct letters followed by 4 distinct nonzero digits,
find the probability of randomly selecting one of these coded items with the first letter a vowel
and the last digit even.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The problem does not say that in the catalog all possible positions are filled,
but I will assume it as a context (by default).
The number of all possible positions is TOTAL = 26*25*24*9*8*7*6,
so this is the number of all possible items in the catalog.
The structure of this formula is clear and does not require more explanations.
To get the number of items with special codes, in the formula above we need
- to replace the total number of letters 26 by the number of vowels 5,
and
- to replace the total number of non-zero digits 9 by the number of nonzero even digits 4.
So, the formula for the number of favorable items becomes FAVORABLE = 5*25*24*4*8*7*6.
The probability under the question is
P =  =  .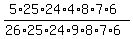
After reducing common factors in the fraction, we get
P =  =  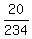= 0.08547 (rounded). ANSWER
Solved.
-------------------
For tutor @greenestamps:
In your response, you should use " 4 " for the number of last non-zero even digits.
--------------------
To a reader:
In his post, @greenestamps writes that there are no restrictions on other letters or digits.
It depends on point of view. The problem says that the letters are distinct and the digits are distinct.
So, I consider it as restrictions.
It is why I wrote my long solution to show explicitly, how to solve the problem accounting for these restrictions.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Of the 26 letters in the alphabet, 5 are vowels: P(1st letter a vowel) = 5/26.
Of the 9 nonzero digits, 5 are even: P(last digits is even) = 5/9.
There are no restrictions on the other letters or digits, so
ANSWER: P((1st letter a vowel) AND (last digit even)) = (5/26)(5/9) = 25/234.
Convert to a decimal or percentage if required
|
|
|
