Question 1207728: I need help with this question, 3p^2-5p-2, I can’t seem to figure out what adds to -5 and multiples to -2
Found 4 solutions by ikleyn, math_tutor2020, mccravyedwin, greenestamps:
Answer by ikleyn(52803)   (Show Source):
You can put this solution on YOUR website! .
The formula says: take 3p^2;
from it, subtract 5p;
from this difference, subtract 2.
Everything is as clear as sunlight at a sunny day.
---------------------
In the future, please do not re-tell your problem in your own words,
because you can not do it in a right way.
Write/copy your problem from your source word-by-word, without any changes.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
It sounds like you want to factor this polynomial.
You have the right idea, but your line of thinking only works if the leading coefficient is 1.
Unfortunately the leading coefficient is 3 instead.
Multiply the leading coefficient with the last term.
3*(-2) = -6
The task of factoring this will have us look for a pair of numbers that
Multiply to -6 AND that add to -5
Let's look at all of the ways to multiply to -6 using two integers (which I'll call m and n).
The first row of this table shows that
-6 * 1 = -6
-6 + 1 = -5
The table is entirely optional. You can find these m,n values through trial-and-error.
Anyways the mystery pair of numbers we want are -6 and 1.
So we'll break the middle term -5p into -6p+1p and apply factor by grouping.
3p^2-5p-2
3p^2-6p+1p-2
(3p^2-6p) + (p-2)
3p(p-2) + 1(p-2)
(3p+1)(p-2)
We've shown that 3p^2-5p-2 fully factors to (3p+1)(p-2)
You can use the FOIL rule to expand (3p+1)(p-2) back to the original expression as a way to verify the answer.
Answer by mccravyedwin(408)  (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Apparently you want to factor this quadratic polynomial.
Suppose that, instead, you are trying to find the solutions to the quadratic equation 
All quadratic equations have two solutions (which might be the same). If the equation is in the form  , then the solutions are given by the quadratic formula:
The equation will have rational roots -- which means the expression will factor into the product of two binomials with rational coefficients -- if and only if the discriminant  is a perfect square.
So, in general, when trying to factor a quadratic polynomial, it might be a good idea to start by verifying that the discriminant is a perfect square.
In your example, we have  , which is a perfect square, so the quadratic should be factorable.
Having verified that, you could continue using the quadratic formula to find the roots of the equation and from there determine how to factor the quadratic expression.
But you apparently are wanting to learn how to do the factoring -- so let's not go by that path.
One response from another tutor has shown you a popular method for doing the factoring, and the response from another tutor shows you a link to where a different quadratic is factored using the same popular method.
I still prefer a different method for factoring that uses a little brain power and logical analysis, rather than following a set process.
Looking at the FOIL method for multiplying binomials, we see
We see that the coefficient of the x^2 term in the product is the product of the coefficients of the linear terms in the two binomials -- ac = a*c; and the constant term in the product is the product of the constant terms in the two binomials -- bd = b*d.
So to find the correct factorization, we look at all the possible ways those conditions can be satisfied.
Now let's look at your example....
The coefficient of the x^2 term in the product is 3: ac=3
The constant term in the product is -2: bd=-2
With ac=3, (and assuming a and c are positive), the only possibility is that a and c are, in some order, 1 and 3.
With bd=-2, the only possibilities are that b and d are, in some order, either 1 and -2, or -1 and 2.
Now consider all the possible combinations of a, b, c, and d and find the one that gives the correct coefficient of x in the product.
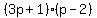
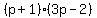
We see that the first factorization is the correct one.
Notice that in that pair, switching the signs of b and d keeps the correct x^2 and constant terms in the product but changes the sign of the middle term.
So if the factorization you tried first was , you would know that the correct factorization is with the signs switched.
We also have, as possible factorizations,
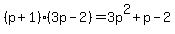
But we don't need to look at those, because we have already found the correct factorization.
|
|
|
