SOLUTION: Solve the inequality. Express your answer using set notation or interval notation. Graph the solution set. 0 < (3x + 6)^(-1) < 1/3

Your starting inequality is

    0 < 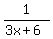 < .    (1)


Left part of this inequality,  0 < 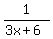,  means that the denominator is positive

    3x + 6 > 0    (otherwise, 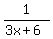   would be negative).


It implies  3x > - 6,  x > 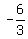 = -2.    (2)


Right part of this inequality is

     < .


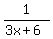Assuming that 3x+6 is positive, we can multiply both sides by 3x+6 without flipping the inequality sign.
By doing it, we get

    1 < ,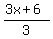

or, equivalently,

    1 < x+2.

It implies 

    x > -1.    (3)


So, we have two inequalities,  (2) and (3).


Therefore, the final answer is  the intersection of these two sets,  x > -1.


In the interval form, the solution set is  (-1,infinity).


This is a graph


   ----|--------|--------(========|========|========|======>
       -3       -2       -1       0        1        2     x