|
Question 1207708: For 0 < a < b, let h be defined by (1/h) = (1/2)[(1/a) + (1/b)].
Show that a < h < b. The number h is called the harmonic mean of a and b.
Found 3 solutions by Edwin McCravy, math_tutor2020, mccravyedwin:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
0 < a < b
a < b
1/a > 1/b
1/b < 1/a
1/b < 1/h < 1/a ..... see note below
b > h > a
a < h < b
Note: 1/h is the midpoint of 1/a and 1/b, due to the formula your teacher gave you.
Therefore, 1/h is guaranteed to be between those values.
A way to prove this can be found through this question
Don't forget to flip the inequality signs when applying reciprocals to all sides.
--------------------------------------------------------------------------
Tutor Edwin has a great approach. I'll paraphrase his method slightly.
Let's rewrite the given formula
1/h = (1/2)*(1/a + 1/b)
1/h = (1/2)*(b/(ab) + a/(ab))
1/h = (1/2)*( (a+b)/(ab) )
1/h = (a+b)/(2ab)
h = 2ab/(a+b)
I'll come back to this later.
Then,
a < b turns into a^2 < ab after multiplying both sides by a
a < b turns into ab < b^2 after multiplying both sides by b
Both a and b are positive, so there's no inequality sign flips when multiplication is applied to both sides.
a^2 < ab & ab < b^2 combine to a^2 < ab < b^2
and finally
a^2 < ab < b^2
a^2+ab < ab+ab < b^2+ab ...... adding ab to all sides
a^2+ab < 2ab < b^2+ab
a(a+b) < 2ab < b(a+b)
a < 2ab/(a+b) < b ........... dividing all sides by (a+b)
a < h < b
Since a > 0 and b > 0, we can be certain that a+b > 0 as well of course.
a+b > 0 means dividing both sides by (a+b) will not flip the inequality sign.
Answer by mccravyedwin(408)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I am tutor Edwin. I have two screen names (Edwin McCravy) and (mccravyedwin)
Here is how I came up with my proof above.
Here is what I did on scratch paper, not something I would post,
or hand in if I were a student.
I simplified this, getting it down to a "flippable" fraction:


 I flipped both sides:
I flipped both sides:
 Then (still on scratch paper), I started with the answer (which
is 'illegal', but you can keep your scratch paper a secret. Your
teacher does not have to see it. Anyway, I worked backwards from
the answer, even though I had no right to do so. LOL
Then (still on scratch paper), I started with the answer (which
is 'illegal', but you can keep your scratch paper a secret. Your
teacher does not have to see it. Anyway, I worked backwards from
the answer, even though I had no right to do so. LOL
    
  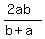   Then I multiplied through by (a+b), reversed from (b+a)
Then I multiplied through by (a+b), reversed from (b+a)
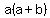  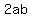  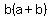
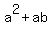  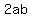  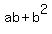 Then I subtracted ab from all three sides:
Then I subtracted ab from all three sides:
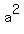  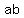  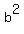 Then I noticed I could make two inequalities out of this:
Then I noticed I could make two inequalities out of this:
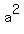  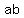 and and 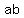  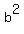 I divided the first through by a, and the second one through by b,
I divided the first through by a, and the second one through by b,
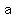   and and    They're both the same. And they're something that was given!!!
Now I must remind you that I had no right to start with the answer
and work backwards. However, by doing so anyway, I was able to reverse
the process and get a process that I did have a right to do.
Now if you will compare what I just did with what I did above, you will
see how I came up with my proof. That is a method that sometimes helps
you to see how to come up with a proof. On scratch paper, start with
the answer, work backwards, then see if you can reverse the steps. Then
toss your scratch paper in the waste basket, and your teacher will never
know. [He/she might suspect though. LOL]
Edwin
They're both the same. And they're something that was given!!!
Now I must remind you that I had no right to start with the answer
and work backwards. However, by doing so anyway, I was able to reverse
the process and get a process that I did have a right to do.
Now if you will compare what I just did with what I did above, you will
see how I came up with my proof. That is a method that sometimes helps
you to see how to come up with a proof. On scratch paper, start with
the answer, work backwards, then see if you can reverse the steps. Then
toss your scratch paper in the waste basket, and your teacher will never
know. [He/she might suspect though. LOL]
Edwin
|
|
|
| |