Question 1207682: For a certain positive integer $n$, the number $n^{6873}$ leaves a remainder of $3$ when divided by $131.$ What remainder does $n$ leave when divided by $131$?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For a certain positive integer $n$, the number $n^{6873}$ leaves a remainder of
$3$ when divided by $131.$ What remainder does $n$ leave when divided by $131$?
~~~~~~~~~~~~~~~~~~~~~~~~~~
After seeing the post by @math_tutor, I found some errors in my previous version
that should be fixed. I fixed them, and now you see my updated version.
Now there is no difference between our final numbers/answers.
We are given that the remainder
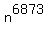 mod 131 is 3.
Notice that 131 is a prime number and 6873 = 113 mod 130.
Now apply the little Fermat's theorem.
It says that for fixed integer "n", where n is relatively prime to 131, the sequence
k --> mod 131 is 3.
Notice that 131 is a prime number and 6873 = 113 mod 130.
Now apply the little Fermat's theorem.
It says that for fixed integer "n", where n is relatively prime to 131, the sequence
k --> 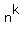 mod 131 is periodical (= cyclic) over integer values k = 1, 2, 3, . . .
with the period of 130.
It tells us that mod 131 is periodical (= cyclic) over integer values k = 1, 2, 3, . . .
with the period of 130.
It tells us that 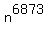 = = 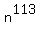 = 3 mod 131.
Based on this information, we should find {n mod 131}.
Let me repeat it again:
Using the little Fermat's theorem, we deduced
from the given info that = 3 mod 131.
Based on this information, we should find {n mod 131}.
Let me repeat it again:
Using the little Fermat's theorem, we deduced
from the given info that 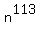 = 3 mod 131.
Having it, we want to find {n mod 131}.
Take = 3 mod 131.
Having it, we want to find {n mod 131}.
Take 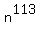 = 3 mod 131 and square it. You will get = 3 mod 131 and square it. You will get 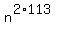 = =  mod 131.
Take mod 131.
Take 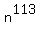 = 3 mod 131 and cube it. You will get = 3 mod 131 and cube it. You will get  = =  mod 131.
. . . and so on . . .
Take mod 131.
. . . and so on . . .
Take 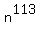 = 3 mod 131 and raise to degree m. You will get = 3 mod 131 and raise to degree m. You will get  = =  mod 131.
The idea is to find a degree m such that m*113 = 1 mod 130.
Then, due to little Fermat's theorem (again) we will have n = mod 131.
The idea is to find a degree m such that m*113 = 1 mod 130.
Then, due to little Fermat's theorem (again) we will have n =  mod 131 and will solve our problem this way.
Thus, our task is to find m, which is
the Modular Multiplicative Inverse to 113 modulo 130.
Fortunately, in the Internet there are calculators for it,
that solve this intermediate task. See these links
Modular Multiplicative Inverse Calculator
https://planetcalc.com/3311/
Inverse Modulo Calculator
https://www.omnicalculator.com/math/inverse-modulo
The Modular Multiplicative Inverse to 113 modulo 130 is 107 modulo 130.
Now the only thing to complete the solution is to find mod 131 and will solve our problem this way.
Thus, our task is to find m, which is
the Modular Multiplicative Inverse to 113 modulo 130.
Fortunately, in the Internet there are calculators for it,
that solve this intermediate task. See these links
Modular Multiplicative Inverse Calculator
https://planetcalc.com/3311/
Inverse Modulo Calculator
https://www.omnicalculator.com/math/inverse-modulo
The Modular Multiplicative Inverse to 113 modulo 130 is 107 modulo 130.
Now the only thing to complete the solution is to find 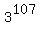 mod 131.
For it, I created Excel spreadsheet below.
The working formula in my spreadsheet is mod 131.
For it, I created Excel spreadsheet below.
The working formula in my spreadsheet is  = =  , ,  = 3.
T A B L E
k = 3.
T A B L E
k 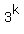 mod 131
------------------------------------
1 3
2 9
3 27
4 81
5 112
6 74
7 91
8 11
9 33
10 99
11 35
12 105
13 53
14 28
15 84
16 121
17 101
18 41
19 123
20 107
21 59
22 46
23 7
24 21
25 63
26 58
27 43
28 129
29 125
30 113
31 77
32 100
33 38
34 114
35 80
36 109
37 65
38 64
39 61
40 52
41 25
42 75
43 94
44 20
45 60
46 49
47 16
48 48
49 13
50 39
51 117
52 89
53 5
54 15
55 45
56 4
57 12
58 36
59 108
60 62
61 55
62 34
63 102
64 44
65 1
66 3
67 9
68 27
69 81
70 112
71 74
72 91
73 11
74 33
75 99
76 35
77 105
78 53
79 28
80 84
81 121
82 101
83 41
84 123
85 107
86 59
87 46
88 7
89 21
90 63
91 58
92 43
93 129
94 125
95 113
96 77
97 100
98 38
99 114
100 80
101 109
102 65
103 64
104 61
105 52
106 25
107 75 <---===
The ANSWER to the problem's question is 75.
In other words, n leaves the remainder 75 when is divided by 131. mod 131
------------------------------------
1 3
2 9
3 27
4 81
5 112
6 74
7 91
8 11
9 33
10 99
11 35
12 105
13 53
14 28
15 84
16 121
17 101
18 41
19 123
20 107
21 59
22 46
23 7
24 21
25 63
26 58
27 43
28 129
29 125
30 113
31 77
32 100
33 38
34 114
35 80
36 109
37 65
38 64
39 61
40 52
41 25
42 75
43 94
44 20
45 60
46 49
47 16
48 48
49 13
50 39
51 117
52 89
53 5
54 15
55 45
56 4
57 12
58 36
59 108
60 62
61 55
62 34
63 102
64 44
65 1
66 3
67 9
68 27
69 81
70 112
71 74
72 91
73 11
74 33
75 99
76 35
77 105
78 53
79 28
80 84
81 121
82 101
83 41
84 123
85 107
86 59
87 46
88 7
89 21
90 63
91 58
92 43
93 129
94 125
95 113
96 77
97 100
98 38
99 114
100 80
101 109
102 65
103 64
104 61
105 52
106 25
107 75 <---===
The ANSWER to the problem's question is 75.
In other words, n leaves the remainder 75 when is divided by 131.
Solved.
------------------
Couple of post-solution notes:
(1) Finding the Modular Multiplicative Inverse to 61 modulo 131 is a technical issue.
I used and referred to online calculators with the only goal do not distract
a reader from the mainstream idea of the solution.
(2) The method making calculations in the spreadsheet is to avoid overflowing (= loosing the precision)
when using direct formula for ( mod 131). mod 131).
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 75
Explanation
We wish to solve an equation of the form
x^k = b (mod n)
for variable x.
To do so, we'll need Euler's totient function.
phi(n) = Euler's totient of n
phi(n) = the number of integers smaller than n that are relatively prime to n.
Examples:
phi(4) = 2 since set S = {1,3} represent values relatively prime to 4 and there are 2 items inside set S.
and
phi(9) = 6 since set S = {1,2,4,5,7,8} represent values relatively prime to 9 and there are 6 items inside set S.
If n is prime, then phi(n) = n-1
Normally the notation is phi(p) = p-1 for some prime p, but I'll stick to n.
In this case 131 is prime which you can check with a list of primes or a computer program/calculator.
So,
phi(131) = 131-1 = 130
k = 6873
b = 3
n = 131
phi(n) = phi(131) = 130
gcd(b,n) = gcd(3,131) = 1
gcd(k,phi(n)) = gcd(6873,130) = 1
The first gcd equation mentioned above is fairly obvious since 3 is not a factor of the prime 131.
Furthermore note how the digits of 131 do not add to a multiple of 3.
The second gcd equation may not be so obvious. Use the Euclidean Algorithm to determine that value. Various online calculators can show the step-by-step process.
Since both gcd(b,n) and gcd(k,phi(n)) are equal to 1, this means we can proceed with the next set of steps below.
If either expression wasn't 1, then we'd have to find another pathway.
----------------------------
Suppose that
x = b^u
is the solution we're after. The goal is to find the value of u.
Apply substitution:
x^k = b (mod n)
(b^u)^k = b (mod n)
b^(uk) = b (mod n)
b^(uk)*b^(-1) = b*b^(-1) (mod n)
b^(uk-1) = 1 (mod n) ............ Let's call this equation (1)
Now we'll apply Euler's Theorem
b^( phi(n) ) = 1 (mod n)
( b^( phi(n) ) )^c = 1^c (mod n)
b^( phi(n)*c ) = 1 (mod n) ............ Let's call this equation (2)
The left hand sides of equations (1) and (2) can be matched up since the right hand sides are both 1.
Furthermore, the exponents match up to show
uk-1 = phi(n)*c
but this is equivalent to saying
uk = 1 ( mod phi(n) )
----------------------------
To recap, we started at the hypothetical endpoint and made up a wish list in saying the solution is of the form x = b^u
Using that and Euler's Theorem we generated these key equations
b^(uk-1) = 1 (mod n)
and
b^( phi(n)*c ) = 1 (mod n)
Then a bit of steps later we arrive at this
uk = 1 ( mod phi(n) )
Then,
uk = 1 ( mod phi(n) )
6873u = 1 ( mod 130)
113u = 1 ( mod 130)
Notice how 6873 = 113 (mod 130)
This is because both 6873 and 113 give the same remainder when dividing by 130.
In other words, 130d = 6873-113 for some integer value of d
--------------------------------------------------------------------------
Now to solve 113u = 1 ( mod 130)
But 113 isn't too far from 130
113 = -17 (mod 130)
113u = 1 (mod 130)
-17u = 1 (mod 130)
That's equivalent to
-17u-1 = 130c
130c+17u = -1
Use the Euclidean Algorithm and back-substitution to determine that one integer solution is: c = -14, u = 107
I'll skip showing steps since various online calculators can show them. This current solution page is getting fairly lengthy as it is.
We go from
130c+17u = -1
to
130*(-14) + 17*(107) = -1
So,
x = b^u (mod 131)
x = 3^107 (mod 131)
x = 75 (mod 131)
How did I jump from 3^107 (mod 131) to 75 (mod 131) ?
Refer to this lesson about Successive Squaring
That lesson in itself is a bit lengthy, but not too bad once you get enough practice at it.
The answer is 75
I used various software tools to verify that the answer is correct.
One quick tool you can use is WolframAlpha
https://www.wolframalpha.com/input?i=3%5E107+%3D+75+%28mod+131%29
and
https://www.wolframalpha.com/input?i=75%5E6873+mod+131
|
|
|