Question 1207668: The distance to the surface of the water in a well can sometimes be found by dropping an object into the well and measuring the time elapsed until a sound is heard. If x is the time (measured in seconds) that it takes for the object to strike the water, than x will obey the equation s = 16x^2, where s is the distance (measured in feet). It follows that x = sqrt{s}/4.
Suppose that y is the time it takes for the sound of the impact to reach your ears. Because sound waves are known to travel at a speed of about 1100 feet per second, the time y to travel the distance s will be y = s/1100. Now x + y is the total time that elapses from the moment that the object is dropped to the moment that a sound is heard.
We have the equation TOTAL TIME ELAPSED = (sqrt{s}/4) + (s/1100).
Find the distance to the water's surface if the total time elapsed from dropping a rock to hearing it hit water is 4 seconds.
Wow! That's a mouth full.
I rearranged the original equation to be
s + 275(sqrt{s}) = 4400
Stick here....
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From this point, you need to solve this equation
s + 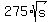 = 4400.
Let u = = 4400.
Let u = 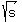 be new variable. Then your equation (1) takes the form
u^2 + 275u = 4400,
or, equivalently,
u^2 + 275u - 4400 = 0.
Apply the quadratic formula be new variable. Then your equation (1) takes the form
u^2 + 275u = 4400,
or, equivalently,
u^2 + 275u - 4400 = 0.
Apply the quadratic formula
 = = 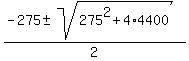 = = 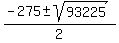 .
You are looking for positive solution "u", so, you accept the positive value, only, and deny the negative one.
So, you have
u = .
You are looking for positive solution "u", so, you accept the positive value, only, and deny the negative one.
So, you have
u = 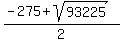 = 15.16384641...
Now you need to find s from equation = 15.16384641...
Now you need to find s from equation 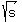 = 15.16384641.
Square both sides and get s = 15.16384641^2 = 229.9422379 feet.
So, the ANSWER is : the distance to the water surface is 230 feet (rounded). = 15.16384641.
Square both sides and get s = 15.16384641^2 = 229.9422379 feet.
So, the ANSWER is : the distance to the water surface is 230 feet (rounded).
That's all: at this point, the problem is just solved to the end.
|
|
|