Question 1207650: Part 1:
Let $f(x)$ and $g(x)$ be polynomials.
Suppose $f(x)=0$ for exactly three values of $x$: namely, $x=-3,4,$ and $8$.
Suppose $g(x)=0$ for exactly five values of $x$: namely, $x=-5,-3,2,4,$ and $8$.
Is it necessarily true that $g(x)$ is divisible by $f(x)$? If so, carefully explain why. If not, give an example where $g(x)$ is not divisible by $f(x)$.
Part 2:
Generalize: for arbitrary polynomials $f(x)$ and $g(x)$, what do we need to know about the zeroes (including complex zeroes) of $f(x)$ and $g(x)$ to infer that $g(x)$ is divisible by $f(x)$?
Found 2 solutions by greenestamps, Edwin McCravy:
Answer by greenestamps(13208)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part 1:
Let $f(x)$ and $g(x)$ be polynomials.
Suppose $f(x)=0$ for exactly three values of $x$: namely, $x=-3,4,$ and $8$.
That means 
Suppose $g(x)=0$ for exactly five values of $x$: namely, $x=-5,-3,2,4,$ and $8$.
That means g(x)=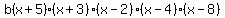
Is it necessarily true that $g(x)$ is divisible by $f(x)$? If so, carefully explain why. If not, give an example where $g(x)$ is not divisible by $f(x)$.
An initial response would say that it is NOT necessarily true that g(x) is divisible by f(x). An example where g(x) is not divisible by f(x) would be with


in which case

Part 2:
Generalize: for arbitrary polynomials $f(x)$ and $g(x)$, what do we need to know about the zeroes (including complex zeroes) of $f(x)$ and $g(x)$ to infer that $g(x)$ is divisible by $f(x)$?
This part of the problem asks us to generalize to determine whether one polynomial is divisible by another solely by looking at the zeroes of the two polynomials.
That implies that the leading coefficients of the two polynomials are irrelevant. That means, in the example above in which I say g(x) is not divisible by f(x), g(x) IS in fact "divisible" by f(x), because the "3/7" in the quotient is "okay".
If we accept the convention that the leading coefficients of the two polynomials do not matter, then the obvious conclusion is that g(x) is divisible by f(x) if (and only if) the set of zeroes of f(x) is a subset of the set of zeroes of g(x).
Answer by Edwin McCravy(20063)   (Show Source): (Show Source):
|
|
|