Question 1207623: Let $m$ and $n$ be positive integers. If $m$ has exactly $10$ positive divisors, $n$ has exactly $16$ positive divisors, and $mn$ has exactly $21$ positive divisors. How many divisors does $m^2 n^2$ have?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let p and q represent unknown prime numbers.
Using the method for finding the number of positive divisors of a number, if mn has 21 positive divisors, then it is either  or or 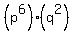 . So the product of m and n contains factors of at most two prime numbers. . So the product of m and n contains factors of at most two prime numbers.
If mn is  , then m and n are both powers of p, but that would make m = , then m and n are both powers of p, but that would make m = 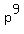 and n = and n =  , in which case mn would be , in which case mn would be 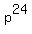 . .
So mn is of the form 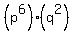 . .
m has 10 positive divisors, and its prime factorization can have at most 2 different primes, and no prime factor can occur more than 6 times. The only possibility is then for m to be of the form 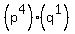 . .
Similarly, n has 16 positive divisors, and its prime factorization can have at most 2 different primes, and no prime factor can occur more than 6 times. The only possibility is then for n to be of the form 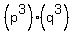 . .
But if mn is of the form 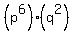 , n can't be of the form , n can't be of the form 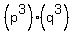 . .
So, while the problem could have been a good one for using math and logical reasoning to find the solution, the given information is inconsistent -- it is impossible for m to have 10 positive divisors, n to have 16, and mn to have 21.
ANSWER: NO SOLUTION
|
|
|