Question 1207618: I run a book club with $n$ people, not including myself. Every day, for $400$ days, I invite $2$ members in the club to review a book. What is the smallest positive integer $n$ so that I can avoid ever having the exact same group of $2$ members over all $400$ days?
Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I run a book club with n people, not including myself. Every day, for 400 days,
I invite 2 members in the club to review a book. What is the smallest positive integer n
so that I can avoid ever having the exact same group of 2 members over all 400 days?
~~~~~~~~~~~~~~~~~~~
It looks to be complicated.
But in reality, it is as simple as a cucumber, and, in addition, it is charming.
When you learn it out, you will gasp . . .
Let the number of the members be n.
Then the number of pairs is  .
They want you find the minimum possible n such that .
They want you find the minimum possible n such that
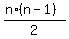 >= 400. (1)
So, all you need is to solve this inequality.
Multiply both sides by 2
n*(n-1) >= 2*400 = 800. (2)
Square root of 800 is 28.2842...
So, your number n is the first integer positive number
which satisfies (2), and it is somewhere close to 28.
Check n= 28: 28*(28-1) = 28*27 = 756 <<<---=== not enough
Check n= 29: 29*(29-1) = 29*28 = 812 <<<---=== just enough
ANSWER. You should have at least 29 members in the club to make it possible. >= 400. (1)
So, all you need is to solve this inequality.
Multiply both sides by 2
n*(n-1) >= 2*400 = 800. (2)
Square root of 800 is 28.2842...
So, your number n is the first integer positive number
which satisfies (2), and it is somewhere close to 28.
Check n= 28: 28*(28-1) = 28*27 = 756 <<<---=== not enough
Check n= 29: 29*(29-1) = 29*28 = 812 <<<---=== just enough
ANSWER. You should have at least 29 members in the club to make it possible.
Solved.
-------------------
Re-phrasing O'Henry, the famous American writer,
The blind begin to walk and the dumb begin to see
when they receive such beautiful solutions to their problems.
|
|
|