SOLUTION: What is the smallest prime divisor of 5^{19} + 7^{13} + 23?

(a)  The prime number 2 is not a divisor of this sum

     (because it is an odd number, as the sum of 3 odd numbers).



(b)  The prime number 3 is not a divisor of this sum.

     Indeed,  5^19 mod 3 = 2^19 mod 3  (because 5 mod 3 is 2).

              The sequence 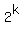 mod 3 is cyclic 2, 1, 2, 1, . . ., and its 19th term is 2.


     Next, 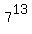    mod 3 =  mod 3   (because 7 mod 3 is 1).

              So, 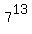  mod 3 is 1.


     Therefore,  5^{19} + 7^{13} + 23 mod 3 is the same as 2 + 1 + 23 mod 3, which is 2.




(c)  The prime number 5 is the prime divisor of  5^{19} + 7^{13} + 23.


     Indeed, the first addend 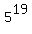   is a multiple of 5;


     Next addend  7^13 mod 5 = 2^13 mod 5  (since 7 mod 5 is 2).
                               
          The sequence 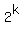  mod 5 is  cyclical 2, 4, 3, 1, 2, 4, 3, 1 . . . with the period length 4;
          
          therefore, 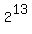  mod 5  is  2.  So,  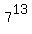 mod5 is 2.


     Now, the sum of three terms  5^{19} + 7^{13} + 23  is 0 + 2 + 24 mod 5, which is the same as 0 mod 5.



Thus 5 is the smallest prime divisor of the sum  5^{19} + 7^{13} + 23.    ANSWER