SOLUTION: Joshua deposited $3560.00 at the beginning of every 6 months for 11 years into a fund paying 3.5% compounded semi-annually. Fourteen years after the first deposit, he then converte

First 11 years, the account accumulates money as annuity-due saving plan, which is deposited
$3560 at the beginning of each 6 months.


Use the standard formula for the future value at the end of this 11-years time period

    FV = 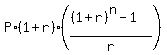,    (1)


where  FV is the future value of the account;  P is the semi-annual payment (deposit) 
at the beginning of each payment period; r is the semi-annual effective percentage 
yield presented as a decimal; n is the number of deposits (= the number of years 
multiplied by 2, or n= 11*2 = 22, in this case).


Under the given conditions, P = 3560;  r = 0.035/2;  n = 11*4 = 44.  
So, according to the formula (1), the future value in 11 years is


    FV = 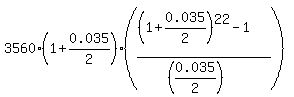 = $96193.53  (rounded).    (2)


Two years after that, on years 12 and 13, the deposits were stopped;
but the amount is still compounded semi-annually;  so, at the end of the 13-th year,
there ae   = 103105.90 dollars on the account.


        Now the account is converted and works as the sinking fund, 
        paying out for 22 years at the beginning of each year.



The formula connecting starting amount of $103105.90 and the annual payouts W  is

    103105.90 = .    (3)


In this formula, calculate the factor separately

     = 13.82115271.    (4)


Now from equation (3),

    W =  = 7460  dollars.


At this point, the solution is complete and the answer is obtained.


ANSWER.  The size of the annual payment is 7460 dollars.