Question 1207543: Suppose $726.56 is deposited at the end of every six months into an account earning 6.45% compounded semi-annually. If the balance in the account four years after the last deposit is to be $31 300.00, how many deposits are needed?
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose $726.56 is deposited at the end of every six months into an account earning 6.45%
compounded semi-annually. If the balance in the account four years after the last deposit
is to be $31 300.00, how many deposits are needed?
~~~~~~~~~~~~~~~~
Use the formula for an Ordinary Annuity saving account compounded semi-annually
FV =  where FV is the future value, P is the payment at the end of every 6 months;
r is the interest rate per year expressed as decimal,
n is the number of semi-annual deposits.
So, we need to find " n " from this equation
where FV is the future value, P is the payment at the end of every 6 months;
r is the interest rate per year expressed as decimal,
n is the number of semi-annual deposits.
So, we need to find " n " from this equation
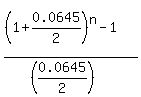 = = 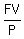 = = 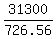 , which is the same as , which is the same as
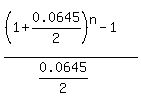 = 43.07971812, = 43.07971812,
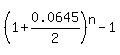 = = 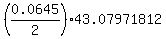 , ,
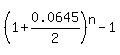 = 1.389320909, = 1.389320909,
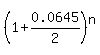 = 1+1.389320909. = 1+1.389320909.
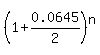 = 2.389320909.
Take logarithm base 10 of both sides
n*log(1+0.0645/12) = log(2.389320909)
and calculate
n = = 2.389320909.
Take logarithm base 10 of both sides
n*log(1+0.0645/12) = log(2.389320909)
and calculate
n = 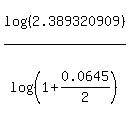 = 27.44 time periods.
Round it to the closest greater integer, which is 28 semi-annual periods,
in order for the bank would be in position to compete the last compounding.
28 semi-annual periods is the same as 14 years.
ANSWER. 14 years. = 27.44 time periods.
Round it to the closest greater integer, which is 28 semi-annual periods,
in order for the bank would be in position to compete the last compounding.
28 semi-annual periods is the same as 14 years.
ANSWER. 14 years.
Solved.
|
|
|