Question 1207429: Keys Company has a target of establishing a fund of$50 OOO. If$10 OOO is deposited at the end of every six months, and the fund earns interest at 4% compounded quarterly, how long will it take to reach the target?
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Keys Company has a target of establishing a fund of $50,000. If $10,000 is deposited
at the end of every six months, and the fund earns interest at 4% compounded quarterly,
how long will it take to reach the target?
~~~~~~~~~~~~~~~~~~~~~
It is a non-traditional accumulative saving plan with $10,000 deposited semi-annually and compounded
quarterly at 4% per annum.
It means that the quarterly effective rate is 0.04/4 = 0.01 and the equivalent
semi-annual effective rate is 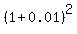 = =  = 1.0201.
+-------------------------------------------------------------------+
| So, this non-traditional accumulative saving plan is equivalent |
| to the ordinary annuity with semi-annual deposits of $10,000 |
| and the semi-annual effective rate of compounding r = 1.0201. |
+-------------------------------------------------------------------+
Now use the general formula for a classic Ordinary Annuity saving plan
FV = = 1.0201.
+-------------------------------------------------------------------+
| So, this non-traditional accumulative saving plan is equivalent |
| to the ordinary annuity with semi-annual deposits of $10,000 |
| and the semi-annual effective rate of compounding r = 1.0201. |
+-------------------------------------------------------------------+
Now use the general formula for a classic Ordinary Annuity saving plan
FV =  , (1)
where FV is the future value of the annuity; P is the semi-annual deposit; r is the semi-annual
effective percentage yield presented as a decimal; n is the number of deposits.
Under the given conditions, P = 10000; r = 0.0201. So, according to (1), the formula for
the future value is
FV = , (1)
where FV is the future value of the annuity; P is the semi-annual deposit; r is the semi-annual
effective percentage yield presented as a decimal; n is the number of deposits.
Under the given conditions, P = 10000; r = 0.0201. So, according to (1), the formula for
the future value is
FV = 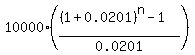 .
So, we should find n, the number of deposits (or the number of semi-annual periods) from this equation
50000 = .
So, we should find n, the number of deposits (or the number of semi-annual periods) from this equation
50000 =  .
Simplify it by dividing both sides by 10000 .
Simplify it by dividing both sides by 10000
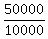 = =  ,
or
5 = ,
or
5 =  .
Simplify it further, step by step
5*0.0201 = .
Simplify it further, step by step
5*0.0201 = 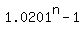 ,
0.1005 = ,
0.1005 = 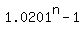 ,
0.1005 + 1 = ,
0.1005 + 1 = 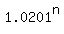 ,
1.1005 = ,
1.1005 = 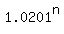 .
Take logarithm base 10 of both sides
log(1.1005) = n*log(1.0201)
and find n
n = .
Take logarithm base 10 of both sides
log(1.1005) = n*log(1.0201)
and find n
n = 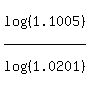 = 4.81 (approximately).
Finally, round the decimal value of 4.81 to the closest GREATER integer value of 5
in order for the bank be in position to complete the last semi-annual compounding.
At this point, the solution is complete.
The ANSWER is: 5 semi-annual periods are needed. = 4.81 (approximately).
Finally, round the decimal value of 4.81 to the closest GREATER integer value of 5
in order for the bank be in position to complete the last semi-annual compounding.
At this point, the solution is complete.
The ANSWER is: 5 semi-annual periods are needed.
-----------------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
|
|
|