Question 1207428: For how many years will Prasad make payments on the $28,000 he borrowed to start his machine shop if he makes payments of $3400 at the end of every three months and interest is 8.08% compounded semi-annually?
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
For how many years will Prasad make payments on the $28,000 he borrowed to start his machine shop
if he makes payments of $3400 at the end of every three months and interest is 8.08% compounded semi-annually?
~~~~~~~~~~~~~~~~~~~~~~~
The scheme of payments/compounding is non-standard and it is not totally clear how to it really works.
So, in my solution I will make some assumptions, but I am not sure if they are adequate.
In any case, I will try.
It is equivalent to semi-annual payments on the loan with semi-annual payments of 2*3400 = 6800 dollars,
while the loan is compounded semi-annually.
So, use the formula for semi-annual payments for a loan
M =  where P is the loan amount; r =
where P is the loan amount; r = 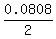 is the effective interest rate semi-annually;
n is the number of payments (same as the number of semi-annual periods);
M is the semi-annual payment of $6800.
In this problem M = 6800; P = $28000; r = is the effective interest rate semi-annually;
n is the number of payments (same as the number of semi-annual periods);
M is the semi-annual payment of $6800.
In this problem M = 6800; P = $28000; r = 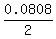 .
Substitute these values into the formula and get for semi-annual payments
6800 = .
Substitute these values into the formula and get for semi-annual payments
6800 = 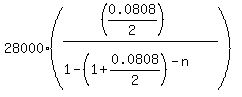 .
We should find "n" from this equation.
Divide both sides by 28000. You will get .
We should find "n" from this equation.
Divide both sides by 28000. You will get
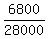 = = 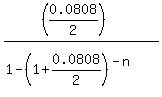 ,
or
0.242857143 = ,
or
0.242857143 = 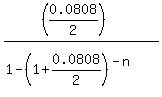 .
It implies, step by step .
It implies, step by step
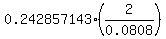 = = 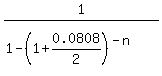 ,
6.011315417 = ,
6.011315417 = 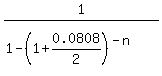 , ,
 = = 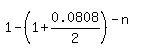 ,
0.166352941 = ,
0.166352941 = 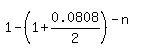 , ,
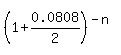 = 1 - 0.166352941, = 1 - 0.166352941,
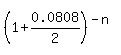 = 0.833647059, = 0.833647059,
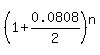 = = 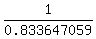 , ,
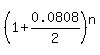 = 1.199548405.
Take logarithm base 10
n*log(1+0.0808/2) = ln(1.199548405)
and find "n"
n = = 1.199548405.
Take logarithm base 10
n*log(1+0.0808/2) = ln(1.199548405)
and find "n"
n = 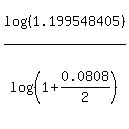 = 4.59.
From these calculations, I make the conclusion that input data in the problem are incorrect,
since they lead to the non-integer number of semi-annual payments. = 4.59.
From these calculations, I make the conclusion that input data in the problem are incorrect,
since they lead to the non-integer number of semi-annual payments.
|
|
|