|
Question 1207426: What payment made at the end of each year for 18 years will amount to $16,000 at 4.2% compounded monthly?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i used the texas instruments business analyst 2 calculator to solve this.
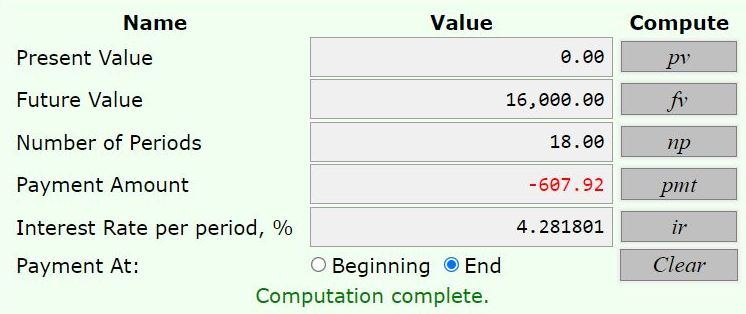
the payment required at the end of each year for 18 years at 4.2% per year compounded monthly is equal to 607.9237653
inputs to the calculator are:
present value = 0
future value = 16000
number of years = 18.
the nominal interest rate per year = 4.2%.
the nominal growth factor is 1.042 per year.
the effective growth factor per month is equal to 1 + .042/12 = 1.0035.
the effective growth factor per year is 1.0035 ^ 12 = 1.042818007.
subtract 1 from this and multiply it by 100 to get an effective interest rate of 4.2818007% per month.
that's what is input to the calculator for the interest rate per time period.
click on payment per time period and you will get 607.9237653.
on online calculator that performs a similar function is found at https://arachnoid.com/finance/index.html
here are the results from using that calculator.
Answer by ikleyn(52855)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What payment made at the end of each year for 18 years will amount to $16,000 at 4.2% compounded monthly?
~~~~~~~~~~~~~~~~~~~~
In his post, tutor @Theo solved this problem using a calculator,
and described a methodology solving this problem using calculator.
It is good, but since this website is intended to teach mathematical methods,
I present here mathematical solution with all detailed explanations.
As it is given in the post, this annuity is not standard: the payments are made at the end of each year,
while compounding is made at the end of each month.
Analytic formulas exist only for coinciding schedules of payments and compounding.
But we can use an equivalent standard synchronized scheme, considering payments at the end of each year
and compounding at the end of each year with the  annual multiplicative growth rate
1+r = annual multiplicative growth rate
1+r = 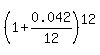 = 1.042818007. (1)
Now we can use a standard formula for such ordinary annuity
FV = = 1.042818007. (1)
Now we can use a standard formula for such ordinary annuity
FV = 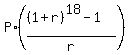 . (2)
In this formula, FV is the future value in 18 years; P is the annual payment, the unknown value
which we should find.
We calculate the factor in the formula (2) separately . (2)
In this formula, FV is the future value in 18 years; P is the annual payment, the unknown value
which we should find.
We calculate the factor in the formula (2) separately
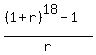 = = 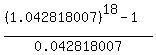 = 26.31908947.
Then from formula (2) we find
P = = 26.31908947.
Then from formula (2) we find
P = 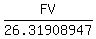 = = 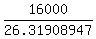 = 607.93 dollars.
Thus we found out the annual payment value. It is $607.93. ANSWER = 607.93 dollars.
Thus we found out the annual payment value. It is $607.93. ANSWER
Solved.
----------------------------------
My result is precisely consisted with the answer by @Theo.
Now you can solve similar problems mathematically and check them using calculator.
It is a good and reliable strategy.
|
|
|
| |