|
Question 1207349: Calculate the purchase price of an annuity paying $200 per month for 10 years with a lump payment of $2000 on the same day as the last payment of $200, at 6.5% compounded monthly.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
Answer by ikleyn(52835)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Calculate the purchase price of an annuity paying $200 per month for 10 years
with a lump payment of $2000 on the same day as the last payment of $200,
at 6.5% compounded monthly.
~~~~~~~~~~~~~~~~~~~~~~~~~
The problem does not say if the regular payments (withdrawals) are made at the beginning or at the end of each month.
Also, from the problem, it is unclear if the lump payment of $2000 does include the last regular payment of $200 or is an addition to it.
Due to this reason, the problem formulation is mathematically lame.
In my solution below, I assume that the regular payments (withdrawals) are made at the end of each month.
I also assume that the lump payment of $2000 is an addition to the last regular payment of $200.
The sough purchase price is the sum of two amounts.
First amount is the starting amount of an annuity that provides paying (from annuity to you) $200 per month for 10 years.
Second amount is the starting amount which provides a lump payment (from the annuity to you) of $2000 in 10 years from now.
To find first amount, use the formula X = 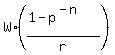 .
In this case, W = $200 is the monthly withdrawal;
r is the effective monthly compounding rate r = 0.065/12;
p = 1 + 0.065/12;
n is the number of withdrawals (the same as the number of months, n = 10*12 = 120).
So,
X = .
In this case, W = $200 is the monthly withdrawal;
r is the effective monthly compounding rate r = 0.065/12;
p = 1 + 0.065/12;
n is the number of withdrawals (the same as the number of months, n = 10*12 = 120).
So,
X = 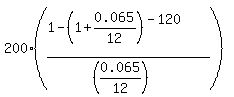 = 17613.70 dollars for the first amount.
To find the value of the second amount, Y, use this equation
2000 = = 17613.70 dollars for the first amount.
To find the value of the second amount, Y, use this equation
2000 =  .
From this equation, Y = .
From this equation, Y = 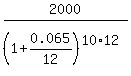 = 1045.924586, or 1045.92 dollars (rounded).
Thus the ANSWER to the problem's question is this sum
X + Y = 17613.70 + 1045.92 = 18659.62 dollars. = 1045.924586, or 1045.92 dollars (rounded).
Thus the ANSWER to the problem's question is this sum
X + Y = 17613.70 + 1045.92 = 18659.62 dollars.
Solved.
|
|
|
| |