Question 1207311: Hi
A car and a van were travelling to town A. The car overtook the van at Point x where they were 126km from town A. The car arrived at town A 3/8 hr earlier than the van while the van was 18km away. Find the average speed of the car and the van.
Found 3 solutions by ikleyn, Theo, greenestamps:
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A car and a van were travelling to town A. The car overtook the van at Point x
where they were 126km from town A. The car arrived at town A 3/8 hr earlier
than the van while the van was 18km away. Find the average speed of the car and the van.
~~~~~~~~~~~~~~~~~~
It is a nice entertainment problem. To solve it,
you should decipher what is hidden in its condition.
The hidden things are these two statements:
(1) the car spent the same time to travel 126 km,
as the van spent to travel 126-18 = 108 km,
and
(2) the van spent 3/8 of an hour to travel 18 km.
From (2), we find the average speed of the van: it is
the distance of 18 km divided by the time 3/8 of an hour = 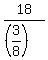 = =  = 6*8 = 48 km/h.
So, half of the problem is just solved for the van.
For the average speed of the car, = 6*8 = 48 km/h.
So, half of the problem is just solved for the van.
For the average speed of the car, 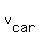 , we write this "time equation" based on (1) , we write this "time equation" based on (1)
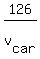 = = 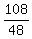 .
From this equation, we find .
From this equation, we find
 = =  = 56 km/h.
At this point, the problem is just solved in full.
ANSWER. The average speed of the car is 56 km/h. The average speed of the van is 48 km/h. = 56 km/h.
At this point, the problem is just solved in full.
ANSWER. The average speed of the car is 56 km/h. The average speed of the van is 48 km/h.
Solved.
---------------------
Re-phrasing a famous American writer O Henry,
the blind begin to walk and the dumb begin to see
when they receive so beautiful solutions to their mathematical problems.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the car catches up to the van when the van is 126 kilometers from town.
the car arrives at the town 3/8 of an hour earlier than the van.
when the car arrives at the town, the van is still 18 kilometers from the town.
as far as i can tell, the starting point for this problem is at point x and the distance traveled from point x to the town is 126 kilometers.
rate * time = distance.
rate for the van is R1.
rate for the car is R2.
time is represented by T.
for the van, you get R1 * T = 126
for the car, you get R2 * (T - 3/8) = 126
also for the van, you get R1 * (T - 3/8) = 108
if you solve for T - 3/8, you get:
T - 3/8 = 126 / R2
T - 3/8 = 108 / R1
since they are both equal to T - 3/8, you get 126 / R2 = 108 / R1
cross multiply to get 126 * R1 = 108 * R2
from that, you get:
R2 / R1 = 126 / 108.
you have R1 * T = 126 and you have R1 * (T - 3/8) = 108
the second equation can be written as R1 * T - 3/8 * R1 = 108
solve for R1 * T in both equations go get:
R1 * T = 126
R1 * T = 3/8 * R1 + 108
since they are both equal to R1 * T, and since R1 * T = 126, you get:
126 = 3/8 * R1 + 108
add 3/8 * R1 to both sides of the equation and subtract 108 from both sides of the equation to get:
126 - 108 = 3/8 * R
simplify to get 18 = 3/8 * R1
solve for R1 to get:
R1 = 18 * 8/3 = 48.
you get R1 = 48 and you get R2 = 126 / 108 * 48 = 56.
that should be your answer.
the average speed of the van is 48 kilometers per hour and the average speed of the car is 56 kilometers per hour.
the van travels 126 kilometers in 126 / 48 = 2.625 hours.
the car travels 126 kilometers in 126 / 56 = 2.25 hours.
the car takes 2.625 minus 2.25 = .375 hours less than the van.
.375 hours is equal to 3/8 hours earlier than the van, as the problem states.
at 56 kilometers per hour, the car takes 2.25 hours to go 126 kilometers.
at 48 kilometers per hour, the van travels 108 kilometers in 2.25 hours.
when the car arrives at the town, the van is 126 minus 108 = 18 kilometers from the town.
the solution appears to be good.
check it out and let me know what you think.
theo
Answer by greenestamps(13195)   (Show Source): (Show Source):
|
|
|