|
Question 1207243: A money box contained some money at first. A took 1/2 the amount of money and another $1500 from the box. After that, B took 1/4 of the remaining amount of money and another $850 from the box. In the end, C took the rest of the money left in the box. Given that C took $1400, find the amount of money in the box at first.
Found 4 solutions by josgarithmetic, ikleyn, greenestamps, MathTherapy:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ikleyn(52814)  (Show Source):
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
This kind of problem is often solved more easily by working backwards, as described below.
C got $1400.
Just before that, B took $850; so before B took $850 the amount was $1400+$850 = $2250.
Just before that, B took 1/4 of the money; that means the $2250 was 3/4 of the money that there was before. So the amount of money before B took 1/4 of it was $2250*(4/3) = $3000.
Just before that, A took $1500; so before A did that the amount was $3000+$1500 = $4500.
And just before that, A took 1/2 of the initial amount; that means the $4500 left after he took 1/2 of the money was also 1/2 of the money. So the initial amount of money was $4500*(2/1) = $9000.
ANSWER: $9000
CHECK:
$9000 minus 1/2 of $9000 = $9000-$4500 = $4500
$4500-$1500 = $3000
$3000 - 1/4 of $3000 = $3000-$750 = $2250
$2250-$850 = $1400
Answer by MathTherapy(10555)  (Show Source):
You can put this solution on YOUR website!
A money box contained some money at first. A took 1/2 the amount of money and another $1500 from the box. After that, B took 1/4 of the remaining amount of money and another $850 from the box. In the end, C took the rest of the money left in the box. Given that C took $1400, find the amount of money in the box at first.
Let original amount be M
After A took 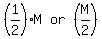 and another $1,500, amount remaining = 
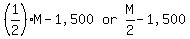After B took  and another $850, amount remaining = 
Now, with C taking the rest of the money - which happens to be $1,400 - we EQUATE the
2 remainders to get: 
3M = 8(3,375) ----- Cross-multiplying
Original amount, or 
|
|
|
| |
