Question 1207217: A person standing 400 ft from the base of a mountain measures the angle of elevation from the ground to the top of the mountain to be 25° The person then walks 500 ft straight back and measures the angle of elevation to now be 20°. How tall is the mountain?
Found 3 solutions by Theo, ikleyn, math_tutor2020:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! 400 feet from the base of the mountain and the angle is 25 degrees.
another 500 feet = 900 feet from the base of the mountain and the angle is 20 degrees.
let x be the height of the mountain.
tan(25) = x/409
tan(20) = x/900.
solve for x in both equations to get:
x = tan(25) * 400 = 186.5230633.
x = tan(20) * 900 = 327.5732108.
there's a problem.
the value of x should have been the same in both equations.
it is not.
assuming the original measurements were correct, there's a problem with either the other angle or the additional feet from the base of the mountain.
if we assume the additional angle is correct, then:
tan(20) = 186.5230633 / y
y is the total feet from the mountain when the angle of elevation is 20 degrees.
solve for y to get y = 186.5230633 / tan(20) = 512.4679045.
the additional distance from the base of the mountain is that minus the original distance = 512.4679045 minus 400 = 112.4679045 feet.
if we assume the additional distance is correct, then:
tan(b) = x / y = 186.5230633 / 900 = .2072478481.
b is the other angle we are looking for that is farther from the base of the mountain.
angle b = arctan (.2072478481) = 11.7086694 degrees.
here's my diagram of the situation as i understand it.

let me know if you have any questions.
theo
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A person standing 400 ft from the base of a mountain measures the angle of elevation
from the ground to the top of the mountain to be 25°. The person then walks 500 ft
straight back and measures the angle of elevation to now be 20°. How tall is the mountain?
~~~~~~~~~~~~~~~~~~~
The solution in the post by @Theo is INCORRECT.
400 feet that Theo marked in his plot, represents, actually, the base of the mountain, which is NOT GIVEN in the problem.
Actually, this data of 400 feet plays small role in this problem (if any) and only confuses a reader.
The data which really PLAYS a role is 500 feet, the distance between the two positions.
I came to bring a correct solution.
Let L be the distance (on the ground level, i.e. horizontally) from the first position to the
top of the mountain. So, we can write
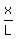 = tan(25°), or x = tan(25°)*L. (1)
where x is the height of the mountain.
Then the distance (on the ground level, i.e. horizontally) from the second position to the
top of the mountain is (L+500) feet. So, we can write = tan(25°), or x = tan(25°)*L. (1)
where x is the height of the mountain.
Then the distance (on the ground level, i.e. horizontally) from the second position to the
top of the mountain is (L+500) feet. So, we can write
 = tan(20°), or x = tan(20°)*(L+500). (2)
In equations (1) and (2) left sides are identical, so their right side are equal
tan(25°)*L = tan(20°)*(L+500).
Simplify and find L
tan(25°)*L = tan(20°)*L + 500*tan(20°),
tan(25°) - tan(20°)*L = 500*tan(20°),
L = = tan(20°), or x = tan(20°)*(L+500). (2)
In equations (1) and (2) left sides are identical, so their right side are equal
tan(25°)*L = tan(20°)*(L+500).
Simplify and find L
tan(25°)*L = tan(20°)*L + 500*tan(20°),
tan(25°) - tan(20°)*L = 500*tan(20°),
L = 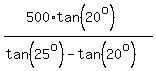 .
Now substitute it into equation (1) and find x
x = .
Now substitute it into equation (1) and find x
x = 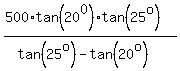 = = 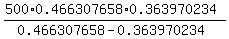 = 829.228 ft.
Round to the closest nearest whole foot and get the
ANSWER. The height of the mountain is about 829 feet. = 829.228 ft.
Round to the closest nearest whole foot and get the
ANSWER. The height of the mountain is about 829 feet.
Solved (correctly).
--------------
To see many other solved similar and different problems of the type " find the height ",
look into the lesson
- Find the height
in this site (free of charge).
Learn the subject from there.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 829.227965 feet (approximate)
Explanation
Review this similar question
https://www.algebra.com/algebra/homework/Triangles/Triangles.faq.question.1199063.html
On that solution page I provide the derivation of this formula
h = d*u*v/(u-v)
where,
h = height of the object
d = distance between observation points
u = tangent of larger angle
v = tangent of smaller angle
In this case,
d = 500
u = tan(25)
v = tan(20)
So we can quickly determine the mountain height to be:
h = d*u*v/(u-v)
h = 500*tan(25)*tan(20)/( tan(25) - tan(20) )
h = 829.227965 feet approximately
Make sure your calculator is in degrees mode.
Tutor Theo incorrectly shows the 400 ft spanning from the original observation point to a point directly under the mountain peak; whereas it should be from the initial observation point to the base of the mountain. Luckily this value is not needed so we can ignore it.
|
|
|